a) Tính độ dài các đoạn \( BC, AH, BH, CH \)

Tính \( BC \):

Vì \( \triangle ABC \) vuông tại A ⇒ dùng định lý Pythagoras:

\[
BC^2 = AB^2 + AC^2 = 6^2 + 8^2 = 36 + 64 = 100
\Rightarrow BC = \sqrt{100} = 10 \, \text{cm}
\]

Tính \( AH \):

Sử dụng công thức diện tích:

- Diện tích tam giác:
\[
S = \frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 6 \cdot 8 = 24 \, \text{cm}^2
\]

- Cũng bằng:
\[
S = \frac{1}{2} \cdot BC \cdot AH \Rightarrow 24 = \frac{1}{2} \cdot 10 \cdot AH
\Rightarrow AH = \frac{24 \cdot 2}{10} = \frac{48}{10} = 4.8 \, \text{cm}
\]

 Tính \( BH \) và \( CH \):

Áp dụng hệ thức lượng trong tam giác vuông:

- \( AB^2 = BH \cdot BC \Rightarrow 36 = BH \cdot 10 \Rightarrow BH = \frac{36}{10} = 3.6 \, \text{cm} \)

- \( AC^2 = CH \cdot BC \Rightarrow 64 = CH \cdot 10 \Rightarrow CH = \frac{64}{10} = 6.4 \, \text{cm} \)

\( BC = 10 \, \text{cm} \)
\( AH = 4.8 \, \text{cm} \)
\( BH = 3.6 \, \text{cm} \)
\( CH = 6.4 \, \text{cm} \)

b) Chứng minh tam giác \( AMN \sim ACB \)

- \( M \) là hình chiếu của \( H \) lên \( AB \) → \( HM \perp AB \)
- \( N \) là hình chiếu của \( H \) lên \( AC \) → \( HN \perp AC \)

⇒ \( AM \perp HM \), \( AN \perp HN \)

Xét tam giác \( AMN \) và tam giác \( ACB \):

- Cả 2 tam giác đều có góc vuông tại \( A \)
- Góc \( \angle MAN \) = góc \( \angle CAB \) (chung đỉnh, chung vị trí góc)

⇒ Tam giác \( AMN \sim ACB \) (g.g)

c) Tính diện tích tứ giác \( BMNC \)

Ta chia tứ giác \( BMNC \) thành 2 tam giác:
- Tam giác \( BMH \)
- Tam giác \( CHN \)

Ta đã biết:
- \( AB = 6, \ AC = 8, \ AH = 4.8 \)
- \( HM \perp AB \), \( HN \perp AC \)

Tính \( AM \):

Tam giác vuông \( AHM \), góc vuông tại \( M \), cạnh góc vuông là:

- \( AM^2 + HM^2 = AH^2 \)

Ta không biết \( HM \), nhưng ta biết góc A là vuông ⇒ đường cao AH chia góc A thành 2 tam giác vuông nhỏ. Tuy nhiên, để đơn giản, ta sẽ dùng công thức tổng quát:

Tính diện tích tứ giác \( BMNC \):

Tứ giác \( BMNC \) là phần còn lại của tam giác \( ABC \) sau khi trừ đi tam giác \( AMN \):

\[
S_{BMNC} = S_{ABC} - S_{AMN}
\]

- \( S_{ABC} = 24 \, \text{cm}^2 \) (đã tính ở trên)
- Tam giác \( AMN \sim ABC \), tỉ số đồng dạng là:
\[
\frac{AM}{AB} = \frac{AH}{AC} = \frac{4.8}{8} = 0.6
\Rightarrow \left( \frac{AM}{AB} \right)^2 = 0.36
\]

⇒ Diện tích \( \triangle AMN = 0.36 \times 24 = 8.64 \, \text{cm}^2 \)

\[
\Rightarrow S_{BMNC} = 24 - 8.64 = 15.36 \, \text{cm}^2
\]

Đáp án c): Diện tích tứ giác \( BMNC = 15.36 \, \text{cm}^2 \)

Chào bạn, mình sẽ giúp bạn giải bài toán này nhé.
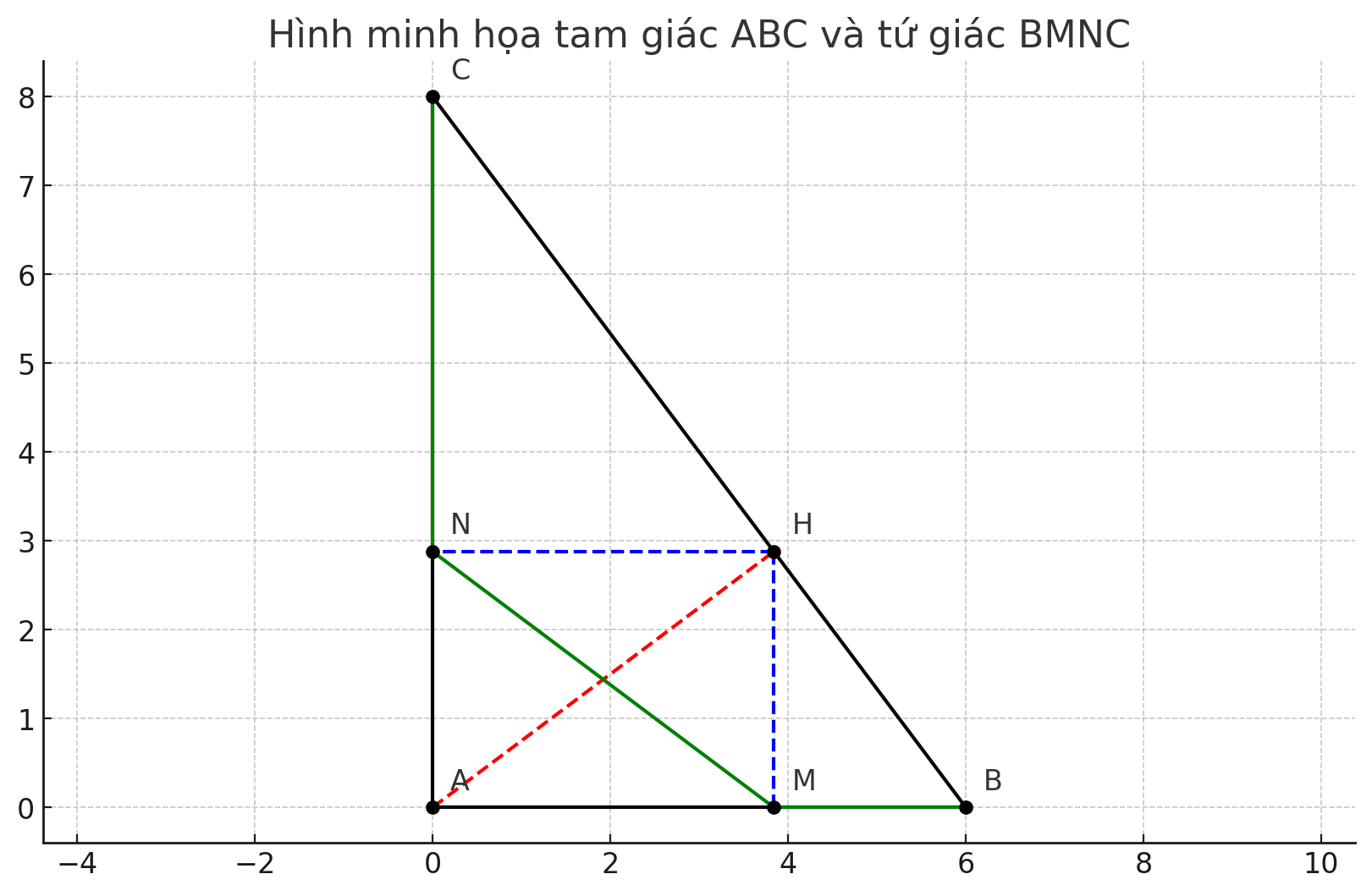
a) Tính BC, AH, BH, CH
* Tính BC: Áp dụng định lý Pytago trong tam giác vuông ABC, ta có:
BC^2 = AB^2 + AC^2 = 6^2 + 8^2 = 36 + 64 = 100
Vậy BC = \sqrt{100} = 10 cm.
* Tính AH: Diện tích tam giác ABC có thể được tính theo hai cách:
\frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot AH \cdot BC
6 \cdot 8 = AH \cdot 10
48 = 10 \cdot AH
Vậy AH = \frac{48}{10} = 4.8 cm.
* Tính BH: Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:
AB^2 = BH \cdot BC
6^2 = BH \cdot 10
36 = 10 \cdot BH
Vậy BH = \frac{36}{10} = 3.6 cm.
* Tính CH: Ta có BC = BH + CH, suy ra:
$$CH = BC - BH = 10 - 3.6 = 6.4$ cm.
b) Chứng minh tam giác AMN đồng dạng với tam giác ACB
* Xét tứ giác AMHN, ta có:
* \angle AMH = 90^\circ (do M là hình chiếu của H trên AB)
* \angle ANH = 90^\circ (do N là hình chiếu của H trên AC)
* \angle MAN = \angle BAC = 90^\circ (gt)
Vậy tứ giác AMHN là hình chữ nhật (tứ giác có ba góc vuông). Suy ra \angle MHN = 90^\circ và AM = HN, AN = HM.
* Xét tam giác AMN và tam giác ACB, ta có:
* \angle MAN = \angle CAB (góc chung)
* \angle AMN = \angle ACB (cùng phụ với \angle NMC). Thật vậy, trong tam giác vuông HMC, \angle NMC + \angle NCH = 90^\circ. Trong tam giác vuông ABC, \angle ABC + \angle ACB = 90^\circ. Mà \angle NMC = \angle ABC (do MH // BC, hai góc đồng vị). Vậy \angle ACB = \angle NMC = \angle AMN.
* Do đó, tam giác AMN đồng dạng với tam giác ACB (g.g).
c) Tính diện tích tứ giác BMNC
Diện tích tứ giác BMNC bằng diện tích tam giác ABC trừ đi diện tích tam giác AMN.
* Diện tích tam giác ABC:
S_{ABC} = \frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 6 \cdot 8 = 24 \, \text{cm}^2
* Diện tích tam giác AMN:
Vì tam giác AMN đồng dạng với tam giác ACB theo tỉ số đồng dạng k = \frac{AH}{BC} = \frac{4.8}{10} = 0.48 (trong tam giác vuông AHC, \sin C = \frac{AH}{AC} = \frac{AN}{AH} \Rightarrow \frac{AN}{AC} = \frac{AH^2}{AC^2}. Tương tự \frac{AM}{AB} = \frac{AH^2}{AB^2}. Tỉ số đồng dạng là \frac{AM}{AB} = \frac{AN}{AC} = \frac{AH}{BC} không đúng. Ta có \angle AMN = \angle ACB và \angle ANM = \angle ABC. Xét \triangle AMN \sim \triangle HNM \sim \triangle CAB).
Ta có AM = AH \cdot \cos(\angle BAH) = AH \cdot \frac{AB}{BC} = 4.8 \cdot \frac{6}{10} = 2.88 cm.
AN = AH \cdot \cos(\angle CAH) = AH \cdot \frac{AC}{BC} = 4.8 \cdot \frac{8}{10} = 3.84 cm.
S_{AMN} = \frac{1}{2} \cdot AM \cdot AN = \frac{1}{2} \cdot 2.88 \cdot 3.84 = 5.5296 \, \text{cm}^2
Hoặc ta có thể dùng tỉ số diện tích:
\frac{S_{AMN}}{S_{ACB}} = \left(\frac{AH}{BC}\right)^2 = \left(\frac{4.8}{10}\right)^2 = 0.48^2 = 0.2304
S_{AMN} = 0.2304 \cdot S_{ACB} = 0.2304 \cdot 24 = 5.5296 \, \text{cm}^2
* Diện tích tứ giác BMNC:
S_{BMNC} = S_{ABC} - S_{AMN} = 24 - 5.5296 = 18.4704 \, \text{cm}^2
Vậy diện tích tứ giác BMNC là 18.4704 \, \text{cm}^2.

Chào bạn, mình sẽ giúp bạn giải bài toán này nhé.
a) Tính BC, AH, BH, CH
* Tính BC: Áp dụng định lý Pytago trong tam giác vuông ABC, ta có:
BC^2 = AB^2 + AC^2 = 6^2 + 8^2 = 36 + 64 = 100
Vậy BC = \sqrt{100} = 10 cm.
* Tính AH: Diện tích tam giác ABC có thể được tính theo hai cách:
\frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot AH \cdot BC
6 \cdot 8 = AH \cdot 10
48 = 10 \cdot AH
Vậy AH = \frac{48}{10} = 4.8 cm.
* Tính BH: Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:
AB^2 = BH \cdot BC
6^2 = BH \cdot 10
36 = 10 \cdot BH
Vậy BH = \frac{36}{10} = 3.6 cm.
* Tính CH: Ta có BC = BH + CH, suy ra:
$$CH = BC - BH = 10 - 3.6 = 6.4$ cm.
b) Chứng minh tam giác AMN đồng dạng với tam giác ACB
* Xét tứ giác AMHN, ta có:
* \angle AMH = 90^\circ (do M là hình chiếu của H trên AB)
* \angle ANH = 90^\circ (do N là hình chiếu của H trên AC)
* \angle MAN = \angle BAC = 90^\circ (gt)
Vậy tứ giác AMHN là hình chữ nhật (tứ giác có ba góc vuông). Suy ra \angle MHN = 90^\circ và AM = HN, AN = HM.
* Xét tam giác AMN và tam giác ACB, ta có:
* \angle MAN = \angle CAB (góc chung)
* \angle AMN = \angle ACB (cùng phụ với \angle NMC). Thật vậy, trong tam giác vuông HMC, \angle NMC + \angle NCH = 90^\circ. Trong tam giác vuông ABC, \angle ABC + \angle ACB = 90^\circ. Mà \angle NMC = \angle ABC (do MH // BC, hai góc đồng vị). Vậy \angle ACB = \angle NMC = \angle AMN.
* Do đó, tam giác AMN đồng dạng với tam giác ACB (g.g).
c) Tính diện tích tứ giác BMNC
Diện tích tứ giác BMNC bằng diện tích tam giác ABC trừ đi diện tích tam giác AMN.
* Diện tích tam giác ABC:
S_{ABC} = \frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 6 \cdot 8 = 24 \, \text{cm}^2
* Diện tích tam giác AMN:
Vì tam giác AMN đồng dạng với tam giác ACB theo tỉ số đồng dạng k = \frac{AH}{BC} = \frac{4.8}{10} = 0.48 (trong tam giác vuông AHC, \sin C = \frac{AH}{AC} = \frac{AN}{AH} \Rightarrow \frac{AN}{AC} = \frac{AH^2}{AC^2}. Tương tự \frac{AM}{AB} = \frac{AH^2}{AB^2}. Tỉ số đồng dạng là \frac{AM}{AB} = \frac{AN}{AC} = \frac{AH}{BC} không đúng. Ta có \angle AMN = \angle ACB và \angle ANM = \angle ABC. Xét \triangle AMN \sim \triangle HNM \sim \triangle CAB).
Ta có AM = AH \cdot \cos(\angle BAH) = AH \cdot \frac{AB}{BC} = 4.8 \cdot \frac{6}{10} = 2.88 cm.
AN = AH \cdot \cos(\angle CAH) = AH \cdot \frac{AC}{BC} = 4.8 \cdot \frac{8}{10} = 3.84 cm.
S_{AMN} = \frac{1}{2} \cdot AM \cdot AN = \frac{1}{2} \cdot 2.88 \cdot 3.84 = 5.5296 \, \text{cm}^2
Hoặc ta có thể dùng tỉ số diện tích:
\frac{S_{AMN}}{S_{ACB}} = \left(\frac{AH}{BC}\right)^2 = \left(\frac{4.8}{10}\right)^2 = 0.48^2 = 0.2304
S_{AMN} = 0.2304 \cdot S_{ACB} = 0.2304 \cdot 24 = 5.5296 \, \text{cm}^2
* Diện tích tứ giác BMNC:
S_{BMNC} = S_{ABC} - S_{AMN} = 24 - 5.5296 = 18.4704 \, \text{cm}^2
Vậy diện tích tứ giác BMNC là 18.4704 \, \text{cm}^2.