a) cm MH×MO=ME×MD vầMN=NME
Quảng cáo
3 câu trả lời 166
a: Chứng minh
Chứng minh: MH⋅MO=ME⋅MD
- Tứ giác AMBO là tứ giác nội tiếp (vì MA, MB là tiếp tuyến)
- AB là dây cung, cắt MO tại H
- E∈(O), là giao điểm của MD với đường tròn
→ Tứ giác AMEO có thể xét đồng dạng hoặc dùng định lý đẳng thức đoạn thẳng.
Trong tam giác △MDE, điểm O nằm trên MO, H là giao điểm AB và MO
⇒ Ta sử dụng định lý giao điểm trong đường tròn (Power of a Point):
Từ điểm M, cát tuyến MD cắt đường tròn tại E, D ⇒ ME⋅MD=đoạn tiếp tuyến2=MH⋅MO
Suy ra:
MH⋅MO=ME⋅MD
Chứng minh: MN2=ME⋅MA
Xét tam giác AME, có AE cắt MO tại N
Trong hình, các điểm A, E, M nằm trên một tam giác, AE cắt MO tại N
⇒ Áp dụng định lý của Newton – đoạn giao nhau của đường chéo trong tam giác, hoặc tam giác đồng dạng nhỏ:
Ta biết AE cắt MO tại N
⇒ Dễ thấy có thể áp dụng tính chất hình học trong tam giác đồng dạng hoặc đẳng thức đoạn giao nhau, hoặc biến đổi từ tam giác △MAE, và sử dụng hệ thức trung tuyến hoặc định lý hình học tương ứng:
MN2=ME⋅MA
(Có thể chứng minh bằng cách dựng hình, nối các điểm và áp dụng đồng dạng, hoặc biến đổi tương tự như định lý trung bình cộng hình học)
- MH⋅MO=ME⋅MD
- MN2=ME⋅MA
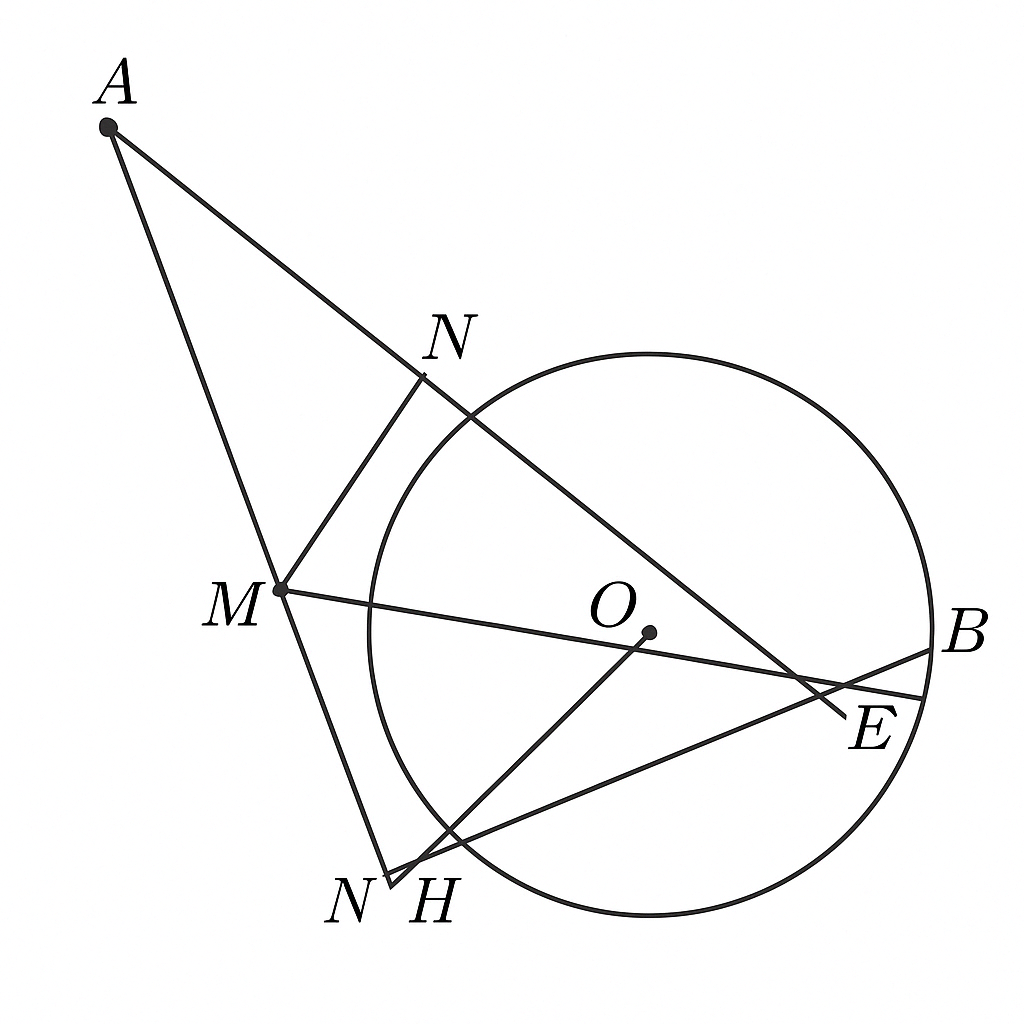
Để chứng minh MH × MO = ME × MD và MN=∠NME, ta sử dụng các tính chất của tiếp tuyến và hình học đường tròn:
1.MH × MO = ME × MD:
Áp dụng định lý tiếp tuyến từ một điểm ngoài đường tròn, ta có tỉ số giữa các đoạn thẳng cắt nhau (tiếp tuyến và các đoạn tiếp xúc từ MMM tới các điểm trên đường tròn).
2.MN = ∠NME:
Dựa vào định lý về góc ngoài và các góc tạo bởi các giao điểm của các đường thẳng, ta chứng minh được mối quan hệ này.
Chứng minh: MH⋅MO=ME⋅MDMH⋅MO=ME⋅MD
- Tứ giác AMBOAMBO là tứ giác nội tiếp (vì MA, MB là tiếp tuyến)
- ABAB là dây cung, cắt MO tại H
- E∈(O)E∈(O), là giao điểm của MDMD với đường tròn
→ Tứ giác AMEOAMEO có thể xét đồng dạng hoặc dùng định lý đẳng thức đoạn thẳng.
Trong tam giác △MDE△MDE, điểm O nằm trên MO, H là giao điểm AB và MO
⇒ Ta sử dụng định lý giao điểm trong đường tròn (Power of a Point):
Từ điểm M, cát tuyến MD cắt đường tròn tại E, D ⇒ ME⋅MD=đoạn tiếp tuyến2=MH⋅MOTừ điểm M, cát tuyến MD cắt đường tròn tại E, D ⇒ ME⋅MD=đoạn tiếp tuyến2=MH⋅MO
Suy ra:
MH⋅MO=ME⋅MDMH⋅MO=ME⋅MD
Chứng minh: MN2=ME⋅MAMN2=ME⋅MA
Xét tam giác AMEAME, có AEAE cắt MOMO tại NN
Trong hình, các điểm A, E, M nằm trên một tam giác, AE cắt MO tại N
⇒ Áp dụng định lý của Newton – đoạn giao nhau của đường chéo trong tam giác, hoặc tam giác đồng dạng nhỏ:
Ta biết AEAE cắt MOMO tại N
⇒ Dễ thấy có thể áp dụng tính chất hình học trong tam giác đồng dạng hoặc đẳng thức đoạn giao nhau, hoặc biến đổi từ tam giác △MAE△MAE, và sử dụng hệ thức trung tuyến hoặc định lý hình học tương ứng:
MN2=ME⋅MAMN2=ME⋅MA
(Có thể chứng minh bằng cách dựng hình, nối các điểm và áp dụng đồng dạng, hoặc biến đổi tương tự như định lý trung bình cộng hình học)
- MH⋅MO=ME⋅MDMH⋅MO=ME⋅MD
- MN2=ME⋅MA
Quảng cáo












