Quảng cáo
2 câu trả lời 138
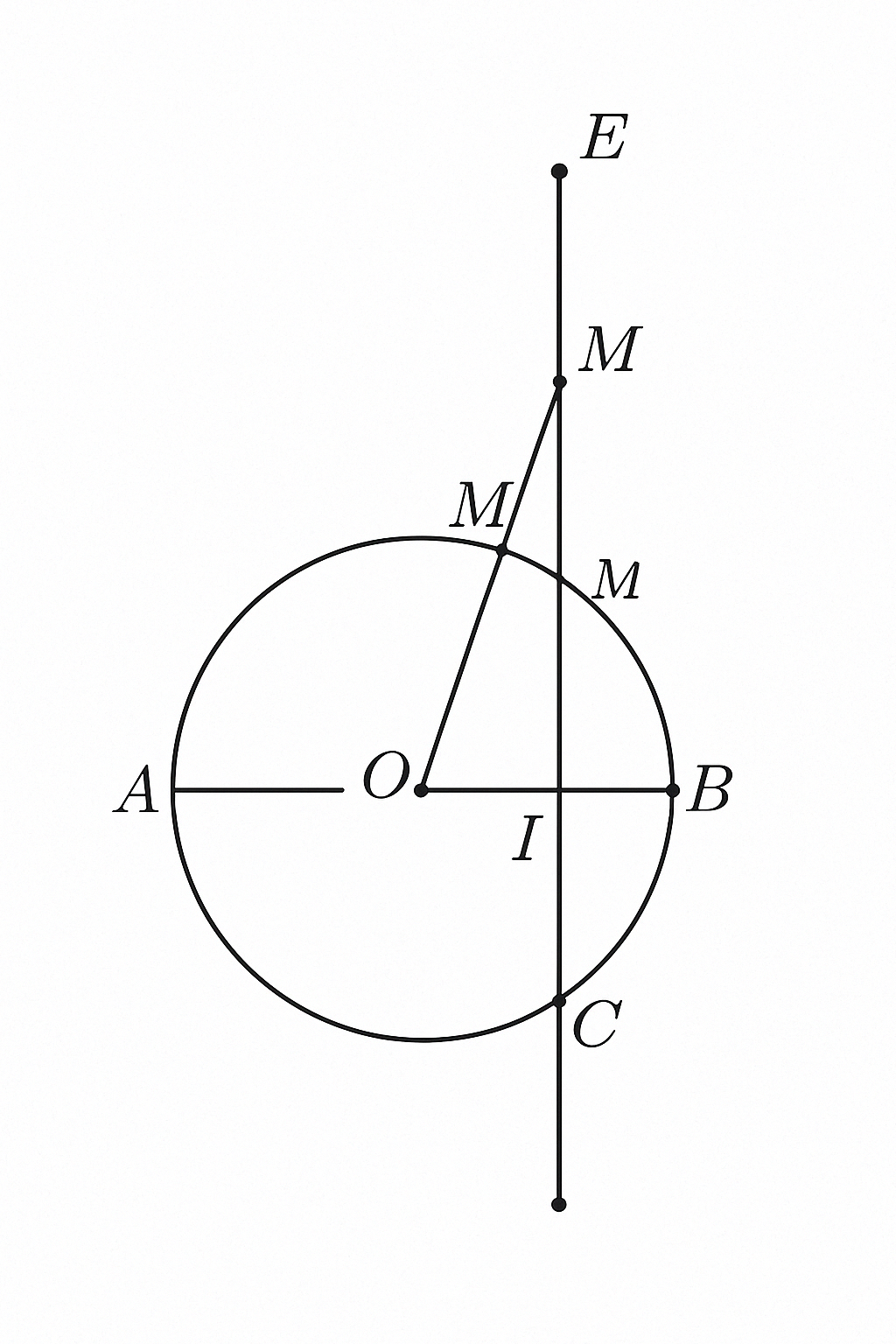
Chứng minh tứ giác \( OCEI \) nội tiếp
Ý tưởng:
- Tứ giác nội tiếp ⇔ Tổng hai góc đối bằng 180°, hoặc cùng nhìn một cung
- \( E \) nằm trên tiếp tuyến tại \( C \), \( OC \) là bán kính vuông góc với tiếp tuyến tại \( C \)
⇒ \( \angle OCE = 90^\circ \)
- \( I \) là trung điểm \( AO \), đường \( EI \perp AO \) tại I ⇒ \( \angle IE O = 90^\circ \)
Hai góc \( \angle OCE = \angle IEO = 90^\circ \)
⇒ Tổng hai góc đối \( = 180^\circ \)
Suy ra: \( OCEI \) là*tứ giác nội tiếp
Chứng minh tứ giác \( IMCB \) nội tiếp
🔹 Phân tích:
- \( \angle ACB = 90^\circ \) (vì \( AB \) là đường kính)
- \( I \) là trung điểm \( AO \), và \( M \) nằm trên đường vuông góc tại I ⇒ \( \angle IMC = 90^\circ \)
➡️ Trong tứ giác \( IMCB \):
- \( \angle IMC = \angle ABC = 90^\circ \)
⇒ Hai góc đối bằng 90° ⇒ Tổng = 180°
Suy ra: \( IMCB \) là tứ giác nội tiếp
- \( OCEI \) là tứ giác nội tiếp vì có hai góc đối vuông ⇒ tổng = 180°
- \( IMCB \) là tứ giác nội tiếp vì có hai góc đối vuông ⇒ tổng = 180°
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387



