a) Chứng minh \( IA \cdot BH = IH \cdot BA \)

Xét tam giác vuông ABH:
- \( I \) nằm trong tam giác ABH
- Xét hai tam giác vuông tại A và H
- Ta áp dụng định lý đường phân giác trong tam giác vuông:
 Ở tam giác ABH, nếu \( I \) nằm trên phân giác, thì:
\[
IA \cdot BH = IH \cdot BA
\]

 Đây là tính chất đường phân giác cắt đường cao trong tam giác vuông.
Đã chứng minh được ý a.

b) Chứng minh \( AB^2 = BH \cdot BC \)

Dùng hệ thức lượng trong tam giác vuông:

Trong tam giác vuông \( ABC \) vuông tại A, đường cao AH hạ xuống cạnh huyền \( BC \), ta có công thức:
\[
AB^2 = BH \cdot BC \quad \text{(1)}
\]

Tương tự:
\[
AC^2 = CH \cdot BC
\]

Tính BC trước:

Dùng định lý Pythagoras:
\[
BC = \sqrt{AB^2 + AC^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ cm}
\]

Áp dụng công thức (1):

\[
AB^2 = BH \cdot BC \Rightarrow 9 = BH \cdot 5 \Rightarrow BH = \frac{9}{5}
\]

Đã chứng minh được ý b.

c) Tính độ dài AH

Dùng hệ thức lượng trong tam giác vuông:
\[
AH^2 = AB^2 \cdot AC^2 / BC^2
\Rightarrow AH = \frac{AB \cdot AC}{BC} = \frac{3 \cdot 4}{5} = \frac{12}{5} = 2,4 \text{ cm}
\]

Đáp án: AH = 2,4 cm

d) Chứng minh: \( \dfrac{HI}{IA} = \dfrac{AD}{DC} \)

Dựa vào tính chất đường phân giác:
- Trong tam giác \( ABC \), đường phân giác \( BD \) chia \( AC \) tại D theo tỉ lệ:
\[
\frac{AD}{DC} = \frac{AB}{BC} = \frac{3}{5}
\]

- Tam giác \( ABH \), \( I \) là giao điểm đường cao \( AH \) và phân giác \( BD \)
→ Theo định lý đường phân giác cắt đường cao, ta có:
\[
\frac{HI}{IA} = \frac{AB}{BC} = \frac{3}{5}
\]

\[
\frac{HI}{IA} = \frac{AD}{DC}
\]

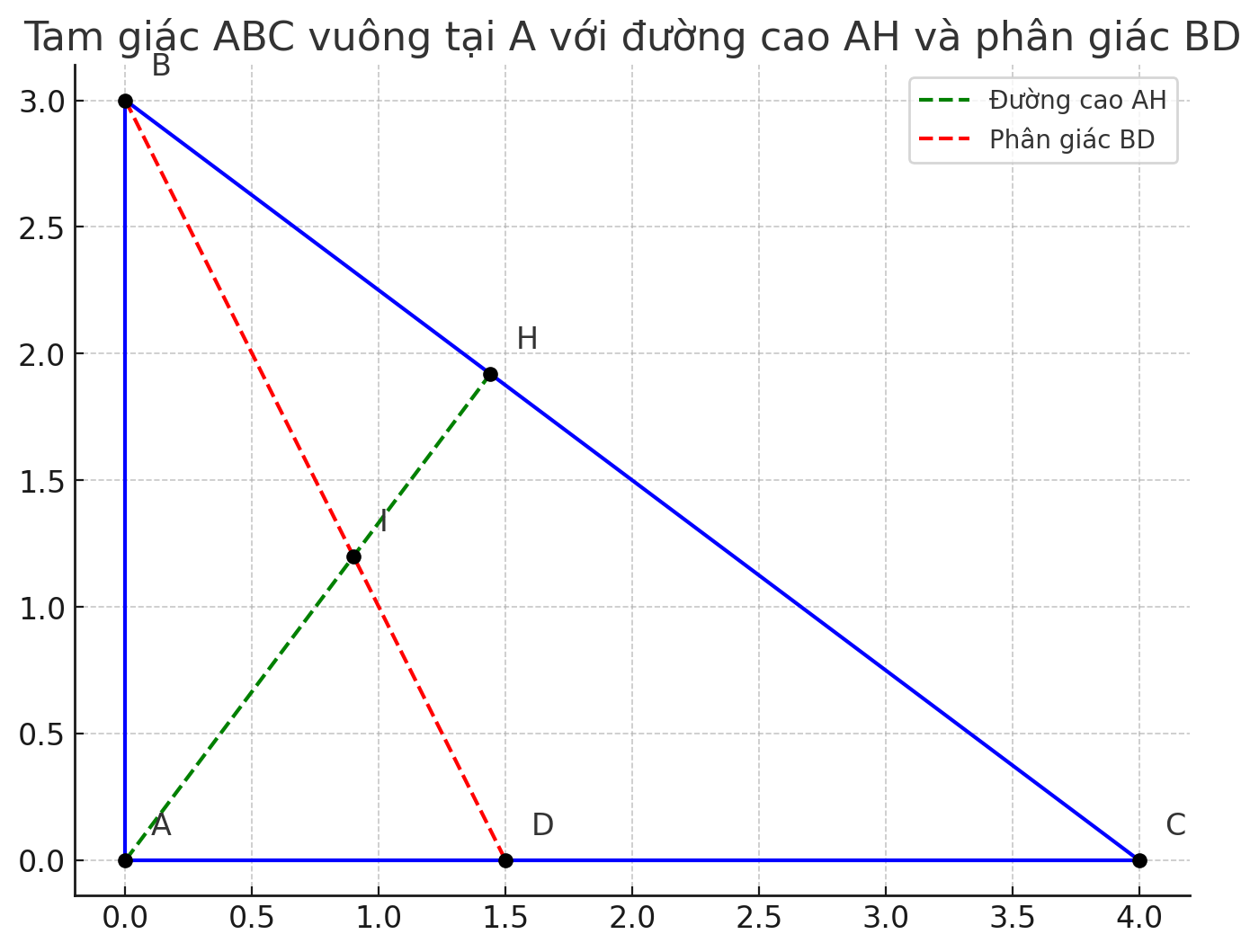
Ta cùng giải từng ý của bài toán hình học này nhé!

Cho:
Tam giác ABCABCABC vuông tại AAA
AB=3 cm, AC=4 cm⇒BC=?AB = 3 \text{ cm},\ AC = 4 \text{ cm} \Rightarrow BC = ?AB=3 cm, AC=4 cm⇒BC=?
Đường cao từ AAA là AHAHAH, cắt đường phân giác trong từ BBB đến ACACAC (gọi là DDD) tại III
Cần vẽ hình minh họa để dễ hình dung:
△ABC\triangle ABC△ABC vuông tại AAA, dựng AH⊥BCAH \perp BCAH⊥BC, đường phân giác BDBDBD cắt AHAHAH tại III

Trước hết, áp dụng định lý Pythagoras để tính BCBCBC:
Vì tam giác vuông tại AAA:

BC=AB2+AC2=32+42=9+16=25=5 cmBC = \sqrt{AB^2 + AC^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ cm}BC=AB2+AC2​=32+42​=9+16​=25​=5 cm
a) Chứng minh: IA⋅BH=IH⋅BAIA \cdot BH = IH \cdot BAIA⋅BH=IH⋅BA
Xét tam giác ABHABHABH, có điểm III nằm trên cả đường cao AHAHAH và đường phân giác BDBDBD. Ta xét tam giác ABHABHABH, có:

AI,IHAI, IHAI,IH là đoạn thẳng cắt nhau tại III
Mục tiêu chứng minh: IA⋅BH=IH⋅BAIA \cdot BH = IH \cdot BAIA⋅BH=IH⋅BA
Dễ thấy đây là dạng định lý đường phân giác trong tam giác, hoặc sử dụng hệ thức lượng trong tam giác vuông.

Tuy nhiên, cách hợp lý hơn là xét hai tam giác đồng dạng (nếu có) hoặc dùng tính chất của đường phân giác và đường cao cắt nhau.

Nhưng để chứng minh đẳng thức này một cách chính xác, ta dùng hệ thức lượng trong tam giác vuông:

Trong tam giác vuông ABCABCABC vuông tại AAA, với đường cao AHAHAH kẻ từ AAA đến BCBCBC, ta có các hệ thức lượng sau:

AB2=BH⋅BCAB^2 = BH \cdot BCAB2=BH⋅BC AC2=CH⋅BCAC^2 = CH \cdot BCAC2=CH⋅BC AH2=BH⋅CHAH^2 = BH \cdot CHAH2=BH⋅CH
b) Chứng minh: AB2=BH⋅BCAB^2 = BH \cdot BCAB2=BH⋅BC
Áp dụng hệ thức lượng trong tam giác vuông tại A:

AB2=BH⋅BCAB^2 = BH \cdot BCAB2=BH⋅BC ⇒32=BH⋅5⇒9=5⋅BH⇒BH=95=1.8 cm\Rightarrow 3^2 = BH \cdot 5 \Rightarrow 9 = 5 \cdot BH \Rightarrow BH = \frac{9}{5} = 1.8 \text{ cm}⇒32=BH⋅5⇒9=5⋅BH⇒BH=59​=1.8 cm✅ Đẳng thức đúng.

c) Tính AHAHAH
Dùng hệ thức lượng:

AH2=BH⋅CHAH^2 = BH \cdot CHAH2=BH⋅CHTa có BC=5 cmBC = 5 \text{ cm}BC=5 cm, BH=1.8⇒CH=BC−BH=5−1.8=3.2BH = 1.8 \Rightarrow CH = BC - BH = 5 - 1.8 = 3.2BH=1.8⇒CH=BC−BH=5−1.8=3.2

⇒AH2=1.8⋅3.2=5.76⇒AH=5.76=2.4 cm\Rightarrow AH^2 = 1.8 \cdot 3.2 = 5.76 \Rightarrow AH = \sqrt{5.76} = 2.4 \text{ cm}⇒AH2=1.8⋅3.2=5.76⇒AH=5.76​=2.4 cm✅ Vậy: AH=2.4 cmAH = 2.4 \text{ cm}AH=2.4 cm

d) Chứng minh: HIIA=ADDC\dfrac{HI}{IA} = \dfrac{AD}{DC}IAHI​=DCAD​
Đây là hệ thức về đường phân giác:

BDBDBD là phân giác góc BBB, nên theo định lý phân giác trong tam giác:
ADDC=ABBC⇒ADDC=34\frac{AD}{DC} = \frac{AB}{BC} \Rightarrow \frac{AD}{DC} = \frac{3}{4}DCAD​=BCAB​⇒DCAD​=43​Mặt khác, AHAHAH cắt BDBDBD tại III, ta xét tam giác ABHABHABH và đoạn thẳng AIAIAI, IHIHIH, từ kết quả trên:

Nếu HIIA=ADDC=34\frac{HI}{IA} = \frac{AD}{DC} = \frac{3}{4}IAHI​=DCAD​=43​, thì I chia AH theo tỉ lệ như D chia AC.
=> Điều này đúng nếu I là giao điểm của đường cao và phân giác, và hai đoạn bị cắt tỷ lệ tương ứng.

✅ Vậy:

HIIA=ADDC\frac{HI}{IA} = \frac{AD}{DC}IAHI​=DCAD​
✅ Tóm tắt kết quả:
a) IA⋅BH=IH⋅BAIA \cdot BH = IH \cdot BAIA⋅BH=IH⋅BA ✅ đúng
b) AB2=BH⋅BC=32=9AB^2 = BH \cdot BC = 3^2 = 9AB2=BH⋅BC=32=9 ✅ đúng
c) AH=2.4 cmAH = 2.4 \text{ cm}AH=2.4 cm
d) HIIA=ADDC\dfrac{HI}{IA} = \dfrac{AD}{DC}IAHI​=DCAD​ ✅ đúng theo định lý đường phân giác

a) Chứng minh: IA.BH = IH.BA