Cho hình bình hành ABCD có Trên cạnh BC lấy M sao cho BM = 4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng DC tại N.
a) Tính tỉ số IB/ID
b) Chứng minh ΔMAB và ΔAND đồng dạng
c) Tính độ dài DN và CN
d) Chứng minh
Quảng cáo
2 câu trả lời 15599

a) AD // BC (gt)![]()
b) Xét ΔAMB và ΔNAD có:
∠BAM = ∠ AND (so le trong, AB // CD)
∠ABM = ∠ADN (góc đối của hình bình hành)
⇒ ΔAMB ∼ ΔNAD (g.g)
c) ΔAMB ∼ ΔNAD (cmt)
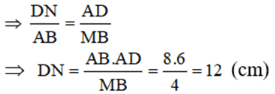
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)
d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
![]()
Tương tự, do AD // BM nên
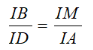
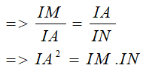
a) AD // BC (gt)
b) Xét ΔAMB và ΔNAD có:
∠BAM = ∠ AND (so le trong, AB // CD)
∠ABM = ∠ADN (góc đối của hình bình hành)
⇒ ΔAMB ∼ ΔNAD (g.g)
c) ΔAMB ∼ ΔNAD (cmt)
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)
d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
Tương tự, do AD // BM nên
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
6354
Đã trả lời bởi chuyên gia
6354 -
 Đã trả lời bởi chuyên gia
4672
Đã trả lời bởi chuyên gia
4672 -
 Đã trả lời bởi chuyên gia
4162
Đã trả lời bởi chuyên gia
4162 -
 Đã trả lời bởi chuyên gia
4108
Đã trả lời bởi chuyên gia
4108


