Phần tự luận (7 điểm)
Cho tam giác ABC (AB < AC), đường phân giác AD. Trên tia đối của tia DA lấy điểm I sao cho ∠ACI = ∠BDA . Chứng minh rằng:
a) ΔADB và ΔACI đồng dạng, ΔADB và ΔCDI đồng dạng
Quảng cáo
1 câu trả lời 5462
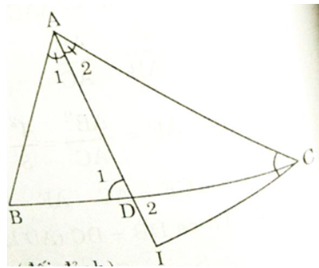
a) Xét ΔABD và ΔACI có:
∠A1 = ∠A2 (AD là tia phân giác ∠BAC)
∠ACI = ∠BDA (gt)
Vậy ΔADB ∼ ΔACI (g.g)
⇒ ∠ABD = ∠AIC (1)
Xét ΔADB và ΔCDI có:
∠ ABD = ∠AIC (chứng minh trên)
∠D1 = ∠D2 (đối đỉnh)
⇒ ΔADB ∼ ΔCDI (g.g)
b) ΔADB ∼ ΔACI (cmt)
![]()
Và ΔADB ∼ ΔCDI
![]()
Từ (1) và (2) ⇒ AB.AC – DB.DC = AD(AI – DI) = AD2 (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
6354
Đã trả lời bởi chuyên gia
6354 -
 Đã trả lời bởi chuyên gia
4672
Đã trả lời bởi chuyên gia
4672 -
 Đã trả lời bởi chuyên gia
4162
Đã trả lời bởi chuyên gia
4162 -
 Đã trả lời bởi chuyên gia
4108
Đã trả lời bởi chuyên gia
4108
Gửi báo cáo thành công!


