Phần tự luận (7 điểm)
Cho tam giác ABC, trung tuyến AD, biết AB = 4cm; AC = 8cm. Qua B dựng đường thẳng cắt AC tại F sao cho góc ABF bằng góc ACB.
a) Chứng tỏ tam giác ABF và tam giác ACB đồng dạng. Tính độ dài đoạn CF
b) Chứng tỏ diện tích tam giác ABC bằng hai lần diện tích tam giác ADC
c) Gọi O là giao điểm của BF và AD, CO cắt AB tại E. Từ A và C lần lượt dựng các đường thẳng song song với BF cắt CO tại J và cắt AD tại I.
+ Chứng tỏ
+ Chứng tỏ
Quảng cáo
1 câu trả lời 4110
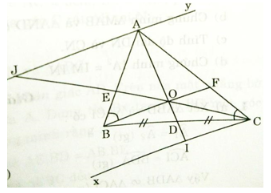
a) Xét ΔABF và ΔABC có :
∠A chung
∠ABF = ∠ACB (gt)
⇒ ΔABF ∼ ΔACB (g.g)
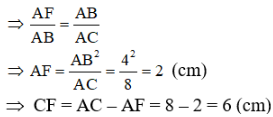
b) Ta có DB = DC (AD là trung tuyến của ΔABC)
![]() (Chung đường cao kẻ từ A và đáy DB = DC)
(Chung đường cao kẻ từ A và đáy DB = DC)
mà ![]()
![]()
c) Ta có Cx // BF (gt). Theo định lí Talét :
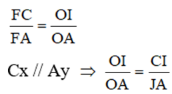
![]()
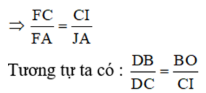
![]()
![]()
Mặt khác Ay//FB ta có:
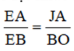
![]()
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
6354
Đã trả lời bởi chuyên gia
6354 -
 Đã trả lời bởi chuyên gia
4672
Đã trả lời bởi chuyên gia
4672 -
 Đã trả lời bởi chuyên gia
4162
Đã trả lời bởi chuyên gia
4162


