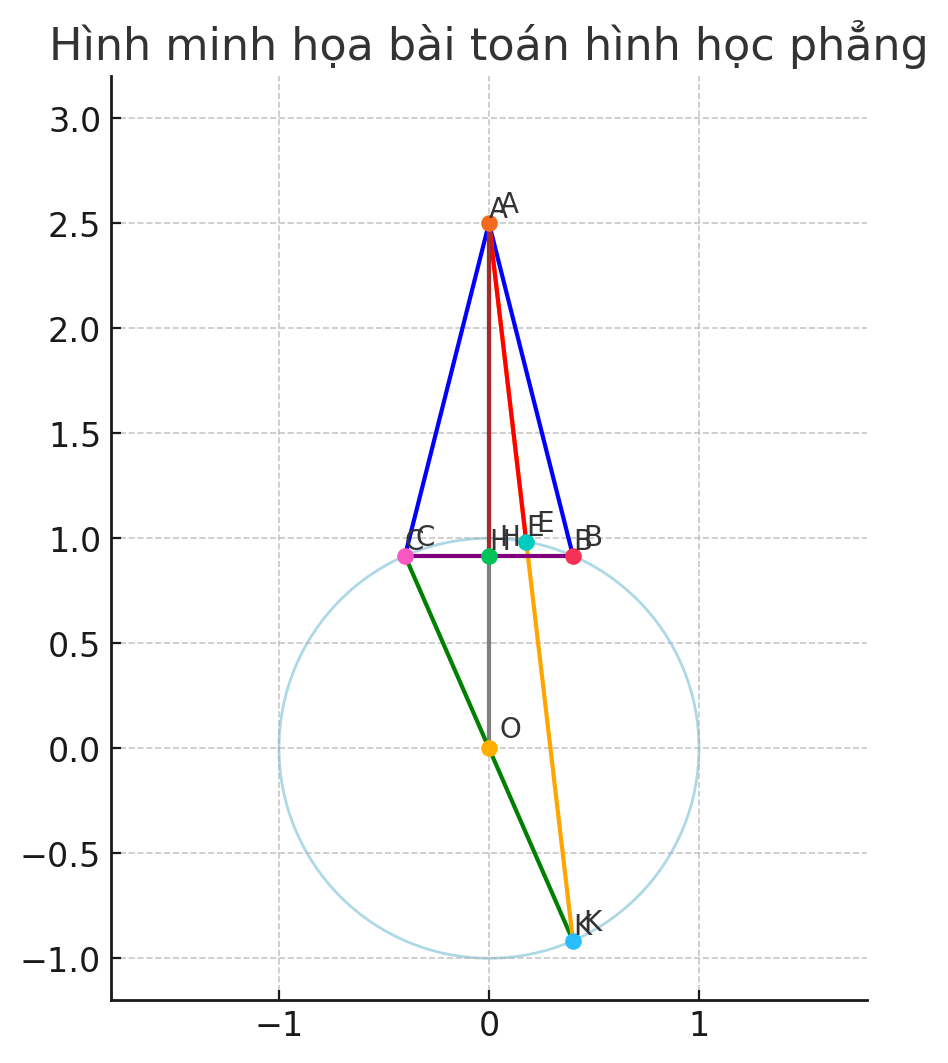
a)C/m OA vuông góc BC và bốn điểm A,B,O,C cùng thuộc 1 đường trong
b) Tính số đo góc KEC và c/m bốn điermr A,E,H,C cùng thuộc 1 đường trong
Quảng cáo
3 câu trả lời 950
a) Chứng minh \( OA \perp BC \) và 4 điểm \( A, B, O, C \) cùng thuộc một đường tròn
Phần 1: Chứng minh \( OA \perp BC \)
- Vì \( AB \) và \( AC \) là tiếp tuyến từ A → \( \angle ABO = \angle ACO = 90^\circ \)
- Tứ giác \( ABOC \) có 2 góc vuông ở B và C
→ ⇒ \( \angle ABO + \angle ACO = 180^\circ \)
→ ⇒ \( ABOC \) là tứ giác nội tiếp
- Gọi H là giao điểm của \( OA \) và \( BC \)
- Xét tam giác vuông \( ABO \) và \( ACO \), có góc vuông tại \( B \) và \( C \), nên hai đường cao từ O đều cùng vuông góc với AB và AC → nên \( OA \) chính là đường trung trực của đoạn \( BC \)
⇒ \( OA \perp BC \) tại trung điểm của \( BC \) ⇒ \( H \in BC \)
Phần 2: Chứng minh \( A, B, O, C \) cùng thuộc một đường tròn
- Vừa chứng minh trên: \( ABOC \) là tứ giác nội tiếp (có 2 góc vuông kề nhau)
⇒ \( \boxed{A, B, O, C} \) cùng thuộc một đường tròn.
b) Tính \( \angle KEC \) và chứng minh \( A, E, H, C \) cùng thuộc một đường tròn
Phần 1: Tính \( \angle KEC \)
- \( CK \) là đường kính ⇒ \( \angle CEK \) chắn nửa đường tròn ⇒ là góc nội tiếp chắn nửa đường tròn ⇒ vuông góc
\[
\boxed{\angle KEC = 90^\circ}
\]
Phần 2: Chứng minh 4 điểm \( A, E, H, C \) cùng thuộc 1 đường tròn
Ta cần chứng minh tứ giác \( AEHC \) nội tiếp.
→ Chứng minh \( \angle AEC + \angle AHC = 180^\circ \)
- Ta có: \( \angle AEC = 90^\circ \) (vừa chứng minh ở trên)
- \( OA \perp BC \) ⇒ \( \angle AHC = 90^\circ \)
⇒ Tổng: \( \angle AEC + \angle AHC = 90^\circ + 90^\circ = 180^\circ \)
⇒ \( \boxed{A, E, H, C} \) cùng thuộc 1 đường tròn
a)
- \( \boxed{OA \perp BC} \)
- \( \boxed{A, B, O, C} \) cùng nằm trên 1 đường tròn
b)
- \( \boxed{\angle KEC = 90^\circ} \)
- \( \boxed{A, E, H, C} \) cùng nằm trên 1 đường tròn
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


