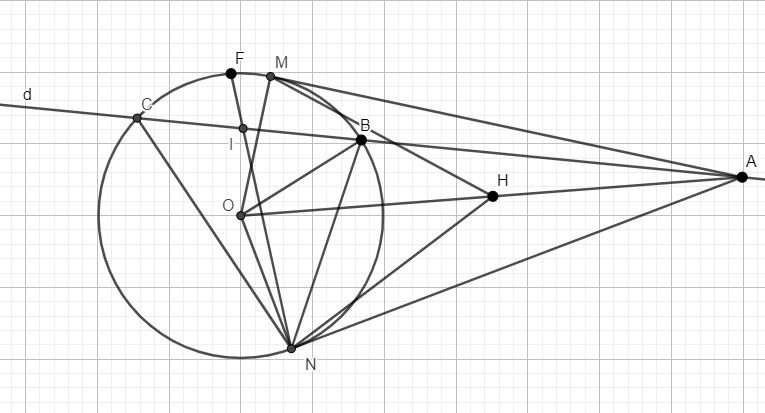
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn. Từ A kẻ hai tiếp tuyến AM, AN với đường tròn (O). Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C ( AB < AC, d không đi qua tâm O ). Gọi I là trung điểm của BC. Đường thẳng NI cắt đường tròn (O) tại điểm thứ hai là F.
a) Chứng minh bốn điểm A, M, O, N cùng thuộc một đường tròn
b) Chứng minh AN² = AB⋅AC và MF // AC
c) Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại K. Chứng minh K thuộc một đường tròn cố định khi d thay đổi.
Quảng cáo
3 câu trả lời 2581
Có AM là tiếp tuyến của đường tròn (O) tại M
=> AM ⊥ OM tại M
=> Δ OAM vuông tại M
Mà MH là đường trung tuyến
=> MH=AH=OH= 1/2 AO (1)
Có AN là tiếp tuyến của đường tròn (O) tại N\
=> AN ⊥ ON tại N
=> Δ OAN vuông tại N
Có AN là đường trung tuyến
=> NH=AH=OH= 1/2 AO (2)
Từ (1) và (2) có MH=NH=AH=OH
=> A,O,N,M cùng ∈ đường tròn (H)
b)
Có OB=ON ( bán kính đường tròn )
=> Δ OBN cân tại O
=> (ONB) ̂ = (OBN) ̂
Có (ONA) ̂ = 90° ( cmt )
=> (ONB) ̂ + (BNA) ̂ = 90°
Có (ANB) ̂ = 90° - (ONB) ̂
Trong Δ OBN có:
(OBN ) ̂+ (BNO) ̂ + (BON) ̂ = 180° ( tổng 3 góc trong Δ )
=> (BON) ̂ = 180° - (OBN) ̂ - (BNO) ̂
=> (BON) ̂ = 180° - 2(ONB) ̂
=> (BON) ̂ = 2(90° - (ONB) ̂)
=> (BON) ̂ = 2(ANB) ̂
=> (ANB) ̂ = 1/2 (BON) ̂ (3)
Có (BCN) ̂ là góc nội tiếp và (BON) ̂ là góc ở tâm cùng chắn ⏜BN của (O)
=> (BCN) ̂ = 1/2 (BON) ̂ (4)
Từ (3) và (4) có (ANB) ̂ = (ACN) ̂
Xét Δ ANB và Δ ANC
(CAN) ̂ chung
(ANB) ̂ = (ACN) ̂
=> ΔANB ̴ ΔACN ( g-g )
=> AN/AC = AB/AN ( các cặp góc tương ứng )
=> AN^2 = AB.AC
Có OB=OC ( bán kính đường tròn )
=> ΔOCB cân ở O
Mà OI là đường trùng tuyến ( vì I là trung điểm BC )
Nên OI đồng thời là đường trung trực của ΔDBC
=> OI ⊥ BC hay OI ⊥ AI tại I
=> (OIA) ̂ = 90°
ΔOIA vuông tại I
=> IH=OH=AH=1/2AO
=> I,O,A ∈ (H)
=> (AIN) ̂ = (AON) ̂ ( 2 góc nội tiếp cùng chắn ⏜AN của (H) (5)
Có AM và AN là 2 tiếp tuyến của (O) cắt nhau tại A
=> OA là tia phân giác của (MON) ̂
=> (MOA) ̂ = (NOA) ̂ = 1/2 (MON) ̂ (6)
Từ (5) và (6) có (AIN) ̂ = 1/2 (MON) ̂ (7)
Trong đường tròn (O) có
(NFM ) ̂là góc nội tiếp, (MON) ̂ là góc ở tâm cùng chắn ⏜MBN
=> (NFM) ̂ = 1/2 (MON) ̂ (8)
Từ (7) và (8) có (AIN) ̂ = (MON) ̂
Mà (AIN) ̂ và (MON) ̂ là 2 góc đồng vị
MF // AC
Có AM là tiếp tuyến của đường tròn (O) tại M
=> AM ⊥ OM tại M
=> Δ OAM vuông tại M
Mà MH là đường trung tuyến
=> MH=AH=OH= 1/2 AO (1)
Có AN là tiếp tuyến của đường tròn (O) tại N\
=> AN ⊥ ON tại N
=> Δ OAN vuông tại N
Có AN là đường trung tuyến
=> NH=AH=OH= 1/2 AO (2)
Từ (1) và (2) có MH=NH=AH=OH
=> A,O,N,M cùng ∈ đường tròn (H)
b)
Có OB=ON ( bán kính đường tròn )
=> Δ OBN cân tại O
=> (ONB) ̂ = (OBN) ̂
Có (ONA) ̂ = 90° ( cmt )
=> (ONB) ̂ + (BNA) ̂ = 90°
Có (ANB) ̂ = 90° - (ONB) ̂
Trong Δ OBN có:
(OBN ) ̂+ (BNO) ̂ + (BON) ̂ = 180° ( tổng 3 góc trong Δ )
=> (BON) ̂ = 180° - (OBN) ̂ - (BNO) ̂
=> (BON) ̂ = 180° - 2(ONB) ̂
=> (BON) ̂ = 2(90° - (ONB) ̂)
=> (BON) ̂ = 2(ANB) ̂
=> (ANB) ̂ = 1/2 (BON) ̂ (3)
Có (BCN) ̂ là góc nội tiếp và (BON) ̂ là góc ở tâm cùng chắn ⏜BN của (O)
=> (BCN) ̂ = 1/2 (BON) ̂ (4)
Từ (3) và (4) có (ANB) ̂ = (ACN) ̂
Xét Δ ANB và Δ ANC
(CAN) ̂ chung
(ANB) ̂ = (ACN) ̂
=> ΔANB ̴ ΔACN ( g-g )
=> AN/AC = AB/AN ( các cặp cạnh tương ứng )
=> AN^2 = AB.AC
Có OB=OC ( bán kính đường tròn )
=> ΔOCB cân ở O
Mà OI là đường trùng tuyến ( vì I là trung điểm BC )
Nên OI đồng thời là đường trung trực của ΔDBC
=> OI ⊥ BC hay OI ⊥ AI tại I
=> (OIA) ̂ = 90°
ΔOIA vuông tại I
=> IH=OH=AH=1/2AO
=> I,O,A ∈ (H)
=> (AIN) ̂ = (AON) ̂ ( 2 góc nội tiếp cùng chắn ⏜AN của (H) (5)
Có AM và AN là 2 tiếp tuyến của (O) cắt nhau tại A
=> OA là tia phân giác của (MON) ̂
=> (MOA) ̂ = (NOA) ̂ = 1/2 (MON) ̂ (6)
Từ (5) và (6) có (AIN) ̂ = 1/2 (MON) ̂ (7)
Trong đường tròn (O) có
(NFM ) ̂là góc nội tiếp, (MON) ̂ là góc ở tâm cùng chắn ⏜MBN
=> (NFM) ̂ = 1/2 (MON) ̂ (8)
Từ (7) và (8) có (AIN) ̂ = (MON) ̂
Mà (AIN) ̂ và (MON) ̂ là 2 góc đồng vị
=> MF // AC ( dhnb )
a) Chứng minh bốn điểm A, M, O, N cùng thuộc một đường tròn
Giải:
Ta có AM và AN là hai tiếp tuyến từ A đến đường tròn (O), vì vậyAM = AN.
Đoạn OM và ON vuông góc với AM và AN tại các điểm tiếp xúc M và N, do tính chất của tiếp tuyến.
Do AM = AN và góc giữa OM và ON đều vuông tại M và N, ta có tam giác OMA vuông tại MM và tam giác ONA vuông tại N.
Do đó, bốn điểm A, M, O, N cùng nằm trên một đường tròn (theo định lý tiếp tuyến và đường tròn).
b) Chứng minh AN² = AB⋅AC và MF // AC
Giải:
Ta có ANAN là tiếp tuyến của đường tròn tại điểm N, và AB, AC là hai đoạn cắt nhau trên đường thẳng d.
Từ tính chất của tiếp tuyến và đoạn cắt, ta có: $AN^2 = AB \cdot AC$
Để chứng minh $MF \parallel AC4, ta xét góc $\angle MAF$ và $\angle MAC$. Theo định lý góc nội tiếp, hai góc này bằng nhau, do đó đường thẳng MF song song với AC.
c) Chứng minh K thuộc một đường tròn cố định khi d thay đổi
Giải:
Hai tiếp tuyến từ điểm B và C đến đường tròn (O) cắt nhau tại điểm K.
Theo định lý tiếp tuyến, điểm K là điểm chung của hai tiếp tuyến từ B và C, và vị trí của điểm K không phụ thuộc vào vị trí cụ thể của điểm B và C trên đường tròn (O).
Vì vậy, điểm K luôn nằm trên một đường tròn cố định, bất kể đường thẳng d thay đổi.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


