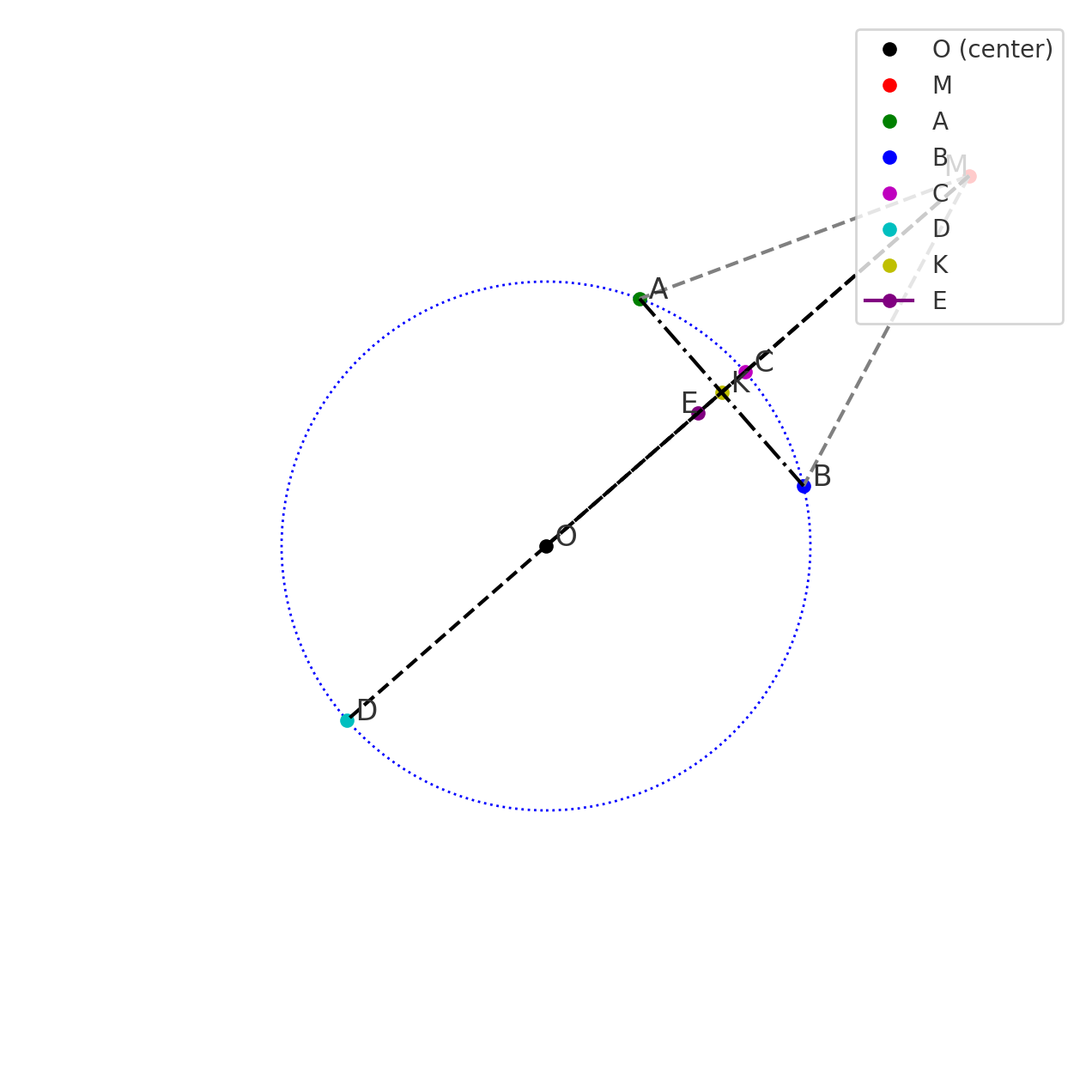
Tính chất của các tiếp tuyến \( MA \) và \( MB \):
- Do \( MA \) và \( MB \) là các tiếp tuyến từ điểm \( M \) đến đường tròn \( (O) \), ta có:
\[
MA = MB
\]
- Điều này dẫn đến \( M \) nằm trên đường trung trực của đoạn \( AB \).

Tính chất của \( O \):
- Vì \( OA = OB \) (bán kính của đường tròn), điểm \( O \) cũng nằm trên đường trung trực của đoạn \( AB \).

Tính chất của đường thẳng \( MO \):
- Từ hai tính chất trên, suy ra \( MO \) là đường trung trực của \( AB \).
- Do đó, \( MO \perp AB \) tại trung điểm \( H \) của đoạn \( AB \).

xd các điểm và góc trong tam giác \( ABD \)

1. Xét điểm \( C \):
- \( C \) là giao điểm của \( MO \) với đường tròn \( (O) \), và nằm giữa \( O \) và \( M \).
- Do \( MO \) là đường trung trực của \( AB \), \( C \) là điểm nằm trên đường cao của tam giác \( ABD \) từ đỉnh \( O \).

2. Định nghĩa điểm \( E \):
- Điểm \( E \) là điểm đối xứng của \( C \) qua điểm \( K \).
- Do đó, \( K \) là trung điểm của \( CE \), và điểm \( E \) sẽ nằm trên đường thẳng kéo dài của đường cao \( CD \) của tam giác \( ABD \).

cm \( E \) là trực tâm của tam giác \( ABD \)

1. cmr  \( E \) là giao điểm của các đường cao của tam giác \( ABD \):
- Trong tam giác \( ABD \), ta đã biết rằng:
- \( MO \) là đường cao từ \( M \) xuống \( AB \) vì \( MO \perp AB \) tại \( H \).
- Đường \( CD \), đi qua \( C \) và vuông góc với \( AB \), là một đường cao khác của tam giác \( ABD \).

2. Đối xứng qua \( K \):
- Điểm \( E \) đối xứng với \( C \) qua \( K \), nên \( E \) nằm trên đường thẳng đi qua \( C \) và vuông góc với \( AB \).
- Do đó, \( E \) chính là giao điểm của các đường cao trong tam giác \( ABD \).

Tính chất của các tiếp tuyến MAMA và MBMB:
- Do MAMA và MBMB là các tiếp tuyến từ điểm MM đến đường tròn (O)(O), ta có:
MA=MBMA=MB
- Điều này dẫn đến MM nằm trên đường trung trực của đoạn ABAB.

Tính chất của OO:
- Vì OA=OBOA=OB (bán kính của đường tròn), điểm OO cũng nằm trên đường trung trực của đoạn ABAB.

Tính chất của đường thẳng MOMO:
- Từ hai tính chất trên, suy ra MOMO là đường trung trực của ABAB.
- Do đó, MO⊥ABMO⊥AB tại trung điểm HH của đoạn ABAB.

xd các điểm và góc trong tam giác ABDABD

1. Xét điểm CC:
- CC là giao điểm của MOMO với đường tròn (O)(O), và nằm giữa OO và MM.
- Do MOMO là đường trung trực của ABAB, CC là điểm nằm trên đường cao của tam giác ABDABD từ đỉnh OO.

2. Định nghĩa điểm EE:
- Điểm EE là điểm đối xứng của CC qua điểm KK.
- Do đó, KK là trung điểm của CECE, và điểm EE sẽ nằm trên đường thẳng kéo dài của đường cao CDCD của tam giác ABDABD.

cm EE là trực tâm của tam giác ABDABD

1. cmr  EE là giao điểm của các đường cao của tam giác ABDABD:
- Trong tam giác ABDABD, ta đã biết rằng:
- MOMO là đường cao từ MM xuống ABAB vì MO⊥ABMO⊥AB tại HH.
- Đường CDCD, đi qua CC và vuông góc với ABAB, là một đường cao khác của tam giác ABDABD.

2. Đối xứng qua KK:
- Điểm EE đối xứng với CC qua KK, nên EE nằm trên đường thẳng đi qua CC và vuông góc với ABAB.
- Do đó, EE chính là giao điểm của các đường cao trong tam giác ABDABD.