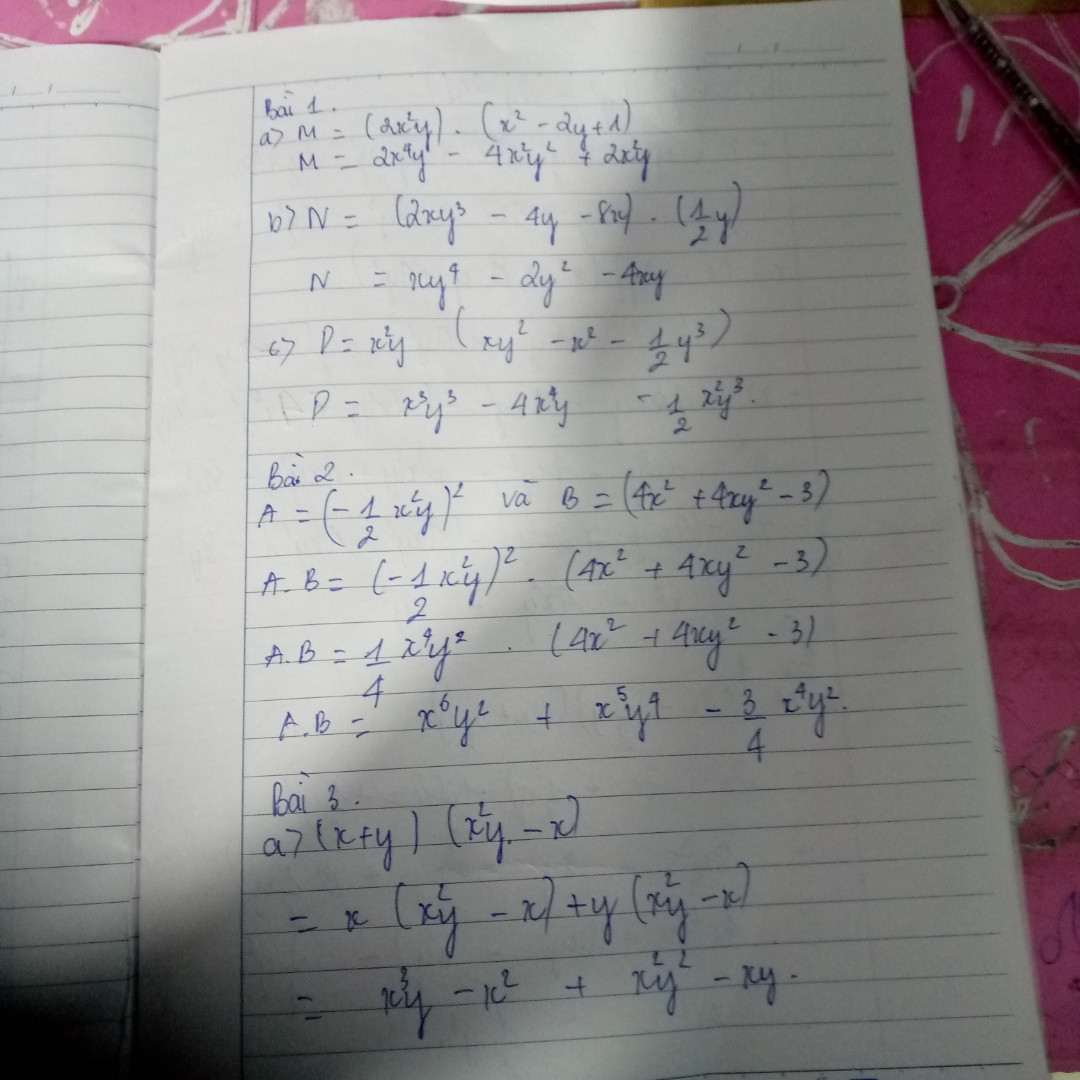**Bài 1: Thực hiện phép nhân**

**a)**
\( M = (2x^3y) \cdot (x^2 - 2y + 1) \)
Phân phối đơn thức \( 2x^3y \) vào từng hạng tử của đa thức:

\[
M = 2x^3y \cdot x^2 - 2x^3y \cdot 2y + 2x^3y \cdot 1
\]
\[
M = 2x^5y - 4x^3y^2 + 2x^3y
\]

**b)**
\( N = (2xy^3 - 4y - 8x) \cdot \left(\frac{1}{2}y\right) \)
Phân phối \( \frac{1}{2}y \) vào từng hạng tử của đa thức:

\[
N = \frac{1}{2}y \cdot 2xy^3 - \frac{1}{2}y \cdot 4y - \frac{1}{2}y \cdot 8x
\]
\[
N = xy^4 - 2y^2 - 4xy
\]

**c)**
\( P = x^2y \cdot (xy^2 - x^2 - \frac{1}{2}y^3) \)
Phân phối \( x^2y \) vào từng hạng tử của đa thức:

\[
P = x^2y \cdot xy^2 - x^2y \cdot x^2 - x^2y \cdot \frac{1}{2}y^3
\]
\[
P = x^3y^3 - x^4y - \frac{1}{2}x^2y^4
\]

---

**Bài 2: Nhân đơn thức A với đa thức B**

\( A = \left(-\frac{1}{2}x^2y\right)^2 \) và \( B = 4x^2 + 4xy^2 - 3 \)

Trước hết, tính \( A \):
\[
A = \left(-\frac{1}{2}x^2y\right)^2 = \frac{1}{4}x^4y^2
\]

Bây giờ nhân \( A \) với \( B \):
\[
A \cdot B = \frac{1}{4}x^4y^2 \cdot (4x^2 + 4xy^2 - 3)
\]
Phân phối \( \frac{1}{4}x^4y^2 \) vào từng hạng tử của \( B \):
\[
= \frac{1}{4}x^4y^2 \cdot 4x^2 + \frac{1}{4}x^4y^2 \cdot 4xy^2 - \frac{1}{4}x^4y^2 \cdot 3
\]
\[
= x^6y^2 + x^5y^4 - \frac{3}{4}x^4y^2
\]

---

**Bài 3: Thực hiện phép nhân**

**a)**
\( (x + y)(x^2y - x) \)
Phân phối \( x + y \) vào từng hạng tử của \( x^2y - x \):

\[
= (x + y) \cdot x^2y - (x + y) \cdot x
\]
\[
= x^3y + x^2y^2 - x^2 - xy
\]

**b)**
\( (x + 2y)(y^2 - 2y + 4z) \)
Phân phối \( x + 2y \) vào từng hạng tử của \( y^2 - 2y + 4z \):

\[
= (x + 2y) \cdot y^2 - (x + 2y) \cdot 2y + (x + 2y) \cdot 4z
\]
\[
= xy^2 + 2y^3 - 2xy - 4y^2 + 4xz + 8yz
\]

**c)**
\( (x - 2y)(x^2 + 2cy + 4y^2) \)
Phân phối \( x - 2y \) vào từng hạng tử của \( x^2 + 2cy + 4y^2 \):

\[
= (x - 2y) \cdot x^2 + (x - 2y) \cdot 2cy + (x - 2y) \cdot 4y^2
\]
\[
= x^3 - 2x^2y + 2cxy - 4cy^2 + 4xy^2 - 8y^3
\]

---

**Bài 4: Rút gọn rồi tính giá trị của biểu thức**

**a)**
\( M = (2x - \frac{1}{2}y)(2x + \frac{1}{2}y) \)

Đây là hiệu và tổng của hai số, áp dụng hằng đẳng thức \( (a - b)(a + b) = a^2 - b^2 \):

\[
M = (2x)^2 - \left(\frac{1}{2}y\right)^2
\]
\[
M = 4x^2 - \frac{1}{4}y^2
\]

Thay \( x = -\frac{1}{2} \) và \( y = 4 \) vào biểu thức:

\[
M = 4\left(-\frac{1}{2}\right)^2 - \frac{1}{4}(4)^2
\]
\[
M = 4 \cdot \frac{1}{4} - \frac{1}{4} \cdot 16
\]
\[
M = 1 - 4 = -3
\]

**b)**
\( N = (2x - y^2)(4x^2 + 2xy^2 + y^4) \)

Thay \( x = \frac{1}{2} \) và \( y = 2 \) vào biểu thức:

\[
N = \left(2\left(\frac{1}{2}\right) - 2^2\right)\left(4\left(\frac{1}{2}\right)^2 + 2\left(\frac{1}{2}\right)(2)^2 + (2)^4\right)
\]
\[
N = (1 - 4)\left(4 \cdot \frac{1}{4} + 2 \cdot \frac{1}{2} \cdot 4 + 16\right)
\]
\[
N = (-3)(1 + 4 + 16)
\]
\[
N = (-3)(21) = -63
\]

Vậy \( N = -63 \).

Dưới đây là các bài toán mà bạn đã yêu cầu:

### Bài 1: Thực hiện phép nhân

**a)** M = (2x³y)(x² - 2y + 1)

- **Tính toán:**
\[
M = 2x³y \cdot x² - 2x³y \cdot 2y + 2x³y \cdot 1
\]
\[
= 2x^{5}y - 4x^{3}y^{2} + 2x³y
\]

Vậy,
\[
M = 2x^{5}y - 4x^{3}y^{2} + 2x³y
\]

**b)** N = (2xy³ - 4y - 8x)(\frac{1}{2}y)

- **Tính toán:**
\[
N = (2xy³)(\frac{1}{2}y) - (4y)(\frac{1}{2}y) - (8x)(\frac{1}{2}y)
\]
\[
= xy^{4} - 2y^{2} - 4xy
\]

Vậy,
\[
N = xy^{4} - 2y^{2} - 4xy
\]

**c)** P = x²y(xy² - x² - \frac{1}{2}y³)

- **Tính toán:**
\[
P = x²y \cdot xy^{2} - x²y \cdot x² - x²y \cdot \frac{1}{2}y^{3}
\]
\[
= x^{3}y^{3} - x^{4}y - \frac{1}{2}x²y^{4}
\]

Vậy,
\[
P = x^{3}y^{3} - x^{4}y - \frac{1}{2}x²y^{4}
\]

### Bài 2: Nhân đơn thức A với đa thức B

**A = (-\frac{1}{2}x²y)² và B = 4x² + 4xy² - 3**

- **Tính toán A:**
\[
A = \left(-\frac{1}{2}x²y\right)² = \frac{1}{4}x^4y^2
\]

- **Nhân A với B:**
\[
A \cdot B = \frac{1}{4}x^4y^2(4x²) + \frac{1}{4}x^4y^2(4xy²) + \frac{1}{4}x^4y^2(-3)
\]
\[
= x^6y^2 + x^5y^4 - \frac{3}{4}x^4y^2
\]

Vậy,
\[
A \cdot B = x^6y^2 + x^5y^4 - \frac{3}{4}x^4y^2
\]

### Bài 3: Thực hiện phép nhân

**a)** (x + y)(x²y - x)

- **Tính toán:**
\[
= x(x²y) + x(-x) + y(x²y) + y(-x)
\]
\[
= x^{3}y - x² + xy^{2} - xy
\]
\[
= x³y + xy² - x² - xy
\]

**b)** (x + 2y)(y² - 2y + 4z)

- **Tính toán:**
\[
= x(y²) + x(-2y) + x(4z) + 2y(y²) + 2y(-2y) + 2y(4z)
\]
\[
= xy^{2} - 2xy + 4xz + 2y^{3} - 4y^{2} + 8yz
\]
\[
= 2y^{3} + xy^{2} - 2xy + 4xz + 8yz - 4y^{2}
\]

**c)** (x - 2y)(x² + 2cy + 4y²)

- **Tính toán:**
\[
= x(x²) + x(2cy) + x(4y²) - 2y(x²) - 2y(2cy) - 2y(4y²)
\]
\[
= x^{3} + 2cxy + 4xy² - 2yx^{2} - 4cy^{2} - 8y^{3}
\]

### Bài 4: Rút gọn rồi tính giá trị của biểu thức

**a)** M = (2x - \frac{1}{2}y)(2x + \frac{1}{2}y) tại X = -\frac{1}{2} và Y = 4

- **Tính toán:**
\[
M = (2x)² - \left(\frac{1}{2}y\right)² = 4x² - \frac{1}{4}y²
\]
Khi x = -\frac{1}{2} và y = 4:
\[
M = 4\left(-\frac{1}{2}\right)^{2} - \frac{1}{4}(4)²
\]
\[
= 4\left(\frac{1}{4}\right) - \frac{1}{4}(16) = 1 - 4 = -3
\]

**b)** N = (2x - y²)(4x² + 2xy² + y⁴) tại X = \frac{1}{2} và Y = 2

- **Tính toán:**
Tính giá trị:
\[
N = (2x)(4x²) + (2x)(2xy²) + (2x)(y⁴) - (y²)(4x²) - (y²)(2xy²) - (y²)(y⁴)
\]
Khi x = \frac{1}{2} và y = 2:
\[
N = (2 * \frac{1}{2} - 2^2)(4(\frac{1}{2})^2 + 2(\frac{1}{2})(2)^2 + 2^4)
\]
\[
= (1 - 4)(1 + 4 + 16) = (-3)(21) = -63
\]

Vậy:
- \(M = -3\)
- \(N = -63\)

Hy vọng những giải thích trên sẽ giúp rõ ràng hơn cho bạn!