Hai xe máy khởi hành cùng một lúc. Xe máy thứ nhất đi từ địa điểm A đến địa điểm B và xe máy thứ hai đi từ địa điểm B đến địa điểm A (trên cùng quãng đường). Tốc độ của xe máy thứ hai bằng ![]() tốc độ của xe máy thứ nhất và sau 2 giờ hai xe gặp nhau. Hỏi mỗi xe đi cả quãng đường AB trong bao lâu?
tốc độ của xe máy thứ nhất và sau 2 giờ hai xe gặp nhau. Hỏi mỗi xe đi cả quãng đường AB trong bao lâu?
Quảng cáo
2 câu trả lời 277
ta có
\[
v_2 = \frac{4}{5}v_1
\]
Hai xe gặp nhau sau 2 h nghĩa là tổng quãng đường mà hai xe đã đi trong 2h bằng quãng đường AB, tức là:
\[
v_1 \times 2 + v_2 \times 2 = S
\]
Thay \( v_2 = \frac{4}{5}v_1 \) vào phương trình trên:
\[
2v_1 + 2 \times \frac{4}{5}v_1 = S
\]
pt
\[
2v_1 + \frac{8}{5}v_1 = S
\]
chuyển
\[
\frac{10}{5}v_1 + \frac{8}{5}v_1 = S
\]
\[
\frac{18}{5}v_1 = S
\]
=> \( S = \frac{18}{5}v_1 \).
Để tìm thời gian mỗi xe đi hết quãng đường AB, ta xét thời gian của từng xe.
Thời gian xe thứ nhất đi hết quãng đường AB:
\[
t_1 = \frac{S}{v_1} = \frac{\frac{18}{5}v_1}{v_1} = \frac{18}{5} = 3,6 \text{ giờ}
\]
Thời gian xe thứ hai đi hết quãng đường AB:
\[
t_2 = \frac{S}{v_2} = \frac{\frac{18}{5}v_1}{\frac{4}{5}v_1} = \frac{18}{4} = 4,5 \text{ giờ}
\]
Gọi x (km/h), y (km/h) lần lượt là tốc độ của xe máy thứ nhất, xe máy thứ hai với x > 0, y > 0.
Theo bài, tốc độ của xe máy thứ hai bằng ![]() tốc độ của xe máy thứ nhất nên ta có phương trình:
tốc độ của xe máy thứ nhất nên ta có phương trình: 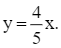
Sau 2 giờ, xe máy thứ nhất đi được quãng đường là: 2x (km) và xe máy thứ hai đi được quãng đường là: 2y (km).
Vì sau 2 giờ hai xe gặp nhau nên ta có:
2x + 2y = AB (trong đó AB là độ dài quãng đường AB).
Ta lập được hệ phương trình: 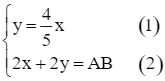
Thế (1) vào phương trình (2), ta nhận được phương trình:
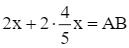
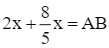
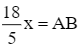
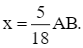
Thay 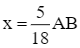 vào phương trình (1), ta được:
vào phương trình (1), ta được:
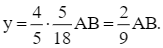
Như vậy, xe máy thứ nhất đi cả quãng đường AB trong: 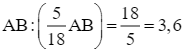 (giờ); xe máy thứ hai đi cả quãng đường AB trong:
(giờ); xe máy thứ hai đi cả quãng đường AB trong: 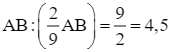 (giờ).
(giờ).
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103437
Đã trả lời bởi chuyên gia
103437 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68807
Đã trả lời bởi chuyên gia
68807 -
 Đã trả lời bởi chuyên gia
56608
Đã trả lời bởi chuyên gia
56608 -
 Đã trả lời bởi chuyên gia
47524
Đã trả lời bởi chuyên gia
47524 -
 Đã trả lời bởi chuyên gia
44249
Đã trả lời bởi chuyên gia
44249 -
 Đã trả lời bởi chuyên gia
36842
Đã trả lời bởi chuyên gia
36842 -
 Đã trả lời bởi chuyên gia
35274
Đã trả lời bởi chuyên gia
35274


