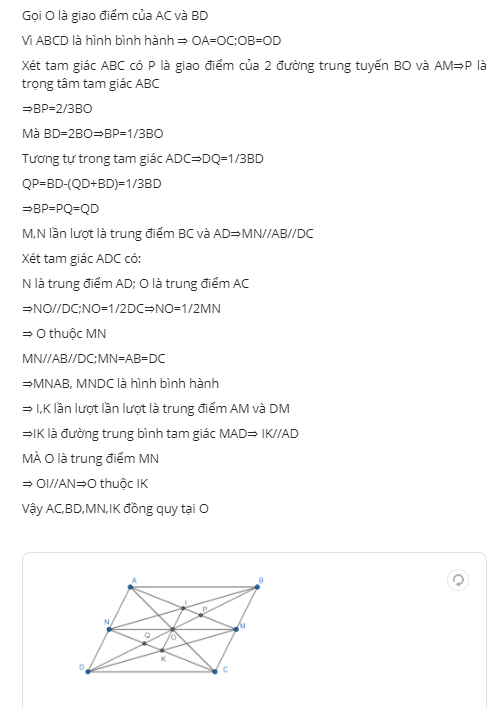
3.2. Cho hình bình hành ABCD . Gọi M, N theo thứ tự là trung điểm của BC, AD. AM cắt BD tai P, CN cắt BD tại Q.
a) Chứng minh BP=PQ=QD
b) Gọi I là giao điểm của AM với BN, K là giao điểm của DM với CN. Chứng minh rằng AC, BD, MN, IK đồng quy
Quảng cáo
3 câu trả lời 2337
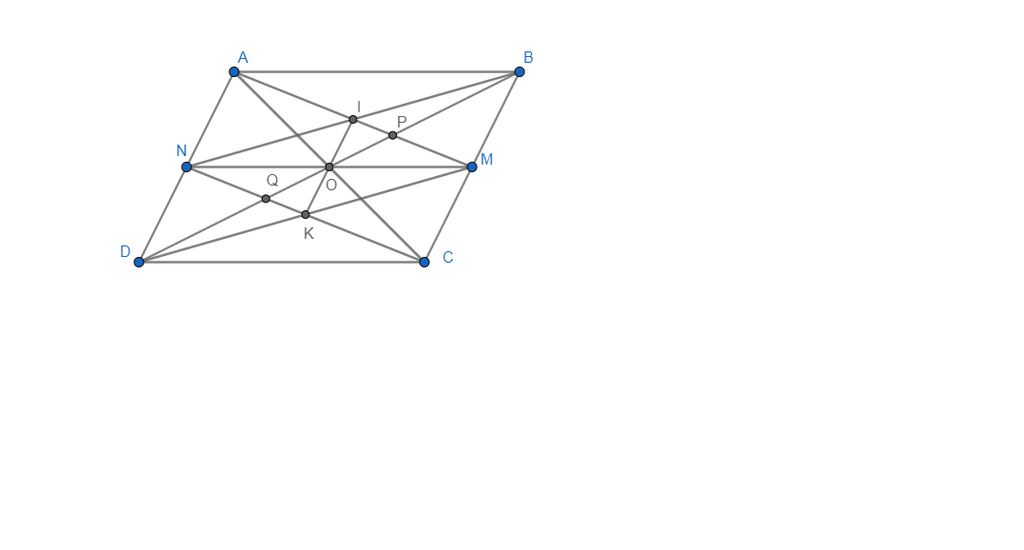
Gọi O là giao điểm của AC và BD
Vì ABCD là hình bình hành ⇒ OA=OC;OB=OD
Xét tam giác ABC có P là giao điểm của 2 đường trung tuyến BO và AM⇒P là trọng tâm tam giác ABC
⇒BP=2/3BO
Mà BD=2BO⇒BP=1/3BO
Tương tự trong tam giác ADC⇒DQ=1/3BD
QP=BD-(QD+BD)=1/3BD
⇒BP=PQ=QD
M,N lần lượt là trung điểm BC và AD⇒MN//AB//DC
Xét tam giác ADC có:
N là trung điểm AD; O là trung điểm AC
⇒NO//DC;NO=1/2DC⇒NO=1/2MN
⇒ O thuộc MN
MN//AB//DC;MN=AB=DC
⇒MNAB, MNDC là hình bình hành
⇒ I,K lần lượt lần lượt là trung điểm AM và DM
⇒IK là đường trung bình tam giác MAD⇒ IK//AD
MÀ O là trung điểm MN
⇒ OI//AN⇒O thuộc IK
Vậy AC,BD,MN,IK đồng quy tại O
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191