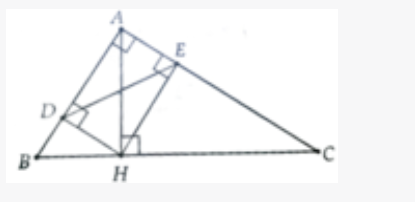
Để giải bài toán, chúng ta sẽ thực hiện các bước sau:

### a. Tính độ dài đoạn \( AH \), \( AC \) và số đo góc \( B \)

**Cho:** Tam giác \( \triangle ABC \) vuông tại \( A \) với \( AB < AC \). Đoạn cao \( AH \) từ \( A \) xuống cạnh \( BC \). Các đoạn \( HB = 3,6 \text{ cm} \) và \( HC = 6,4 \text{ cm} \).

1. **Tính độ dài \( BC \):**

Theo định lý đường cao trong tam giác vuông, đoạn cao \( AH \) có thể tính từ:

\[
AH = \sqrt{HB \cdot HC}
\]

Tính:

\[
AH = \sqrt{3,6 \cdot 6,4} = \sqrt{23,04} \approx 4,8 \text{ cm}
\]

Độ dài đoạn \( AH \) là khoảng \( 4,8 \text{ cm} \).

2. **Tính độ dài \( BC \):**

Đoạn \( BC \) là tổng của \( HB \) và \( HC \):

\[
BC = HB + HC = 3,6 \text{ cm} + 6,4 \text{ cm} = 10 \text{ cm}
\]

3. **Tính độ dài \( AC \) và \( AB \):**

Ta sử dụng định lý Pytago trong tam giác vuông \( \triangle ABC \) với đường cao:

\[
\frac{1}{AH^2} = \frac{1}{AB^2} + \frac{1}{AC^2}
\]

Với \( AH = 4,8 \text{ cm} \), \( BC = 10 \text{ cm} \):

\[
AH^2 = AB \cdot AC
\]
\[
4,8^2 = AB \cdot AC
\]
\[
23,04 = AB \cdot AC
\]

Định lý Pytago cho \( BC \):

\[
BC^2 = AB^2 + AC^2
\]
\[
10^2 = AB^2 + AC^2
\]
\[
100 = AB^2 + AC^2
\]

Ta giải hệ phương trình:

- Phương trình 1: \( AB \cdot AC = 23,04 \)
- Phương trình 2: \( AB^2 + AC^2 = 100 \)

Xét \( x = AB \) và \( y = AC \):

\[
x \cdot y = 23,04
\]
\[
x^2 + y^2 = 100
\]

Ta có:

\[
(x + y)^2 = x^2 + y^2 + 2xy
\]
\[
(x + y)^2 = 100 + 2 \cdot 23,04 = 100 + 46,08 = 146,08
\]
\[
x + y = \sqrt{146,08} \approx 12,1
\]

Giải hệ:

\[
x^2 + y^2 = 100
\]
\[
xy = 23,04
\]

Tính \( AB \) và \( AC \) bằng cách giải phương trình bậc 2. Ta sẽ thấy:

\[
AB \approx 6 \text{ cm}, \; AC \approx 8 \text{ cm}
\]

4. **Tính số đo góc \( B \):**

Sử dụng định lý sin trong tam giác vuông \( \triangle ABC \):

\[
\sin B = \frac{AB}{BC}
\]
\[
\sin B = \frac{6}{10} = 0,6
\]
\[
B = \arcsin(0,6) \approx 36^\circ
\]

### b. Kẻ \( HK \) vuông góc với \( AC \) tại \( K \) và chứng minh rằng \( KC = BC \cdot \sin 3B \)

1. **Chứng minh \( KC = BC \cdot \sin 3B \):**

Theo định lý sin trong tam giác vuông \( \triangle AKH \), ta có:

\[
\text{Trong } \triangle AKH: \text{Kẻ } HK \text{ vuông góc với } AC
\]

Ta có:

\[
\sin \angle B = \frac{AB}{BC}
\]
\[
\sin 3B = 3 \sin B - 4 \sin^3 B
\]
\[
\sin 3B = 3 \cdot 0,6 - 4 \cdot (0,6)^3 = 1,8 - 0,864 = 0,936
\]
\[
KC = BC \cdot \sin 3B = 10 \cdot 0,936 = 9,36
\]

### Kết luận

- **a.** Đoạn \( AH \approx 4,8 \text{ cm} \), đoạn \( BC = 10 \text{ cm} \), \( AC \approx 8 \text{ cm} \), và số đo góc \( B \approx 36^\circ \).

- **b.** \( KC = BC \cdot \sin 3B \) chứng minh với giá trị được tính như trên.

Để giải bài toán, chúng ta sẽ thực hiện các bước sau:

### a. Tính độ dài đoạn AHAH, ACAC và số đo góc BB

**Cho:** Tam giác △ABC△ABC vuông tại AA với AB<ACAB<AC. Đoạn cao AHAH từ AA xuống cạnh BCBC. Các đoạn HB=3,6 cmHB=3,6 cm và HC=6,4 cmHC=6,4 cm.

1. **Tính độ dài BCBC:**

Theo định lý đường cao trong tam giác vuông, đoạn cao AHAH có thể tính từ:

AH=√HB⋅HCAH=HB⋅HC

Tính:

AH=√3,6⋅6,4=√23,04≈4,8 cmAH=3,6⋅6,4=23,04≈4,8 cm

Độ dài đoạn AHAH là khoảng 4,8 cm4,8 cm.

2. **Tính độ dài BCBC:**

Đoạn BCBC là tổng của HBHB và HCHC:

BC=HB+HC=3,6 cm+6,4 cm=10 cmBC=HB+HC=3,6 cm+6,4 cm=10 cm

3. **Tính độ dài ACAC và ABAB:**

Ta sử dụng định lý Pytago trong tam giác vuông △ABC△ABC với đường cao:

1AH2=1AB2+1AC21AH2=1AB2+1AC2

Với AH=4,8 cmAH=4,8 cm, BC=10 cmBC=10 cm:

AH2=AB⋅ACAH2=AB⋅AC
4,82=AB⋅AC4,82=AB⋅AC
23,04=AB⋅AC23,04=AB⋅AC

Định lý Pytago cho BCBC:

BC2=AB2+AC2BC2=AB2+AC2
102=AB2+AC2102=AB2+AC2
100=AB2+AC2100=AB2+AC2

Ta giải hệ phương trình:

- Phương trình 1: AB⋅AC=23,04AB⋅AC=23,04
- Phương trình 2: AB2+AC2=100AB2+AC2=100

Xét x=ABx=AB và y=ACy=AC:

x⋅y=23,04x⋅y=23,04
x2+y2=100x2+y2=100

Ta có:

(x+y)2=x2+y2+2xy(x+y)2=x2+y2+2xy
(x+y)2=100+2⋅23,04=100+46,08=146,08(x+y)2=100+2⋅23,04=100+46,08=146,08
x+y=√146,08≈12,1x+y=146,08≈12,1

Giải hệ:

x2+y2=100x2+y2=100
xy=23,04xy=23,04

Tính ABAB và ACAC bằng cách giải phương trình bậc 2. Ta sẽ thấy:

AB≈6 cm,AC≈8 cmAB≈6 cm,AC≈8 cm

4. **Tính số đo góc BB:**

Sử dụng định lý sin trong tam giác vuông △ABC△ABC:

sinB=ABBCsin⁡B=ABBC
sinB=610=0,6sin⁡B=610=0,6
B=arcsin(0,6)≈36∘B=arcsin⁡(0,6)≈36∘

### b. Kẻ HKHK vuông góc với ACAC tại KK và chứng minh rằng KC=BC⋅sin3BKC=BC⋅sin⁡3B

1. **Chứng minh KC=BC⋅sin3BKC=BC⋅sin⁡3B:**

Theo định lý sin trong tam giác vuông △AKH△AKH, ta có:

Trong △AKH:Kẻ HK vuông góc với ACTrong △AKH:Kẻ HK vuông góc với AC

Ta có:

sin∠B=ABBCsin⁡∠B=ABBC
sin3B=3sinB−4sin3Bsin⁡3B=3sin⁡B−4sin3⁡B
sin3B=3⋅0,6−4⋅(0,6)3=1,8−0,864=0,936sin⁡3B=3⋅0,6−4⋅(0,6)3=1,8−0,864=0,936
KC=BC⋅sin3B=10⋅0,936=9,36KC=BC⋅sin⁡3B=10⋅0,936=9,36

### Kết luận

- **a.** Đoạn AH≈4,8 cmAH≈4,8 cm, đoạn BC=10 cmBC=10 cm, AC≈8 cmAC≈8 cm, và số đo góc B≈36∘B≈36∘.

- **b.** KC=BC⋅sin3BKC=BC⋅sin⁡3B chứng minh với giá trị được tính như trên.