Question

Đã trả lời bởi chuyên gia

Answer 1

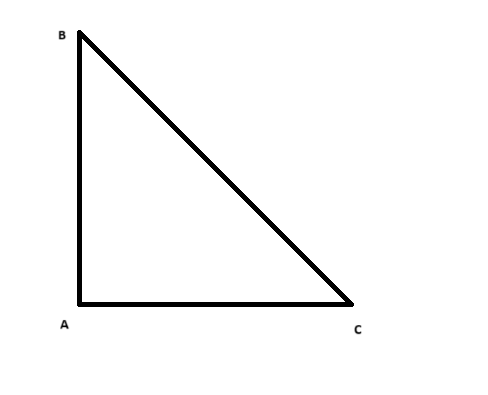
Trong tam giác vuông ABC với $\angle A = 90^\circ$ và $\angle C = 45^\circ$, điều đó có nghĩa là $\angle B = 45^\circ$ (vì tổng của ba góc trong tam giác bằng $180^\circ$).

Do đó, tam giác vuông ABC là tam giác vuông đều, với hai góc vuông bằng nhau (45 độ).

Tính độ dài các cạnh

Trong một tam giác vuông đều, các cạnh có một số tính chất đặc biệt:

1. Tính cạnh huyền BC:

Trong một tam giác vuông với góc $45^\circ$, các cạnh đối diện hai góc $45^\circ$ bằng nhau. Do đó, ta có thể sử dụng định lý Pythagoras để tính cạnh huyền.

Định lý Pythagoras cho tam giác vuông ABC là:
\[
BC^2 = AB^2 + AC^2
\]

Trong tam giác vuông đều, $AB = AC$, do đó:
\[
BC^2 = AB^2 + AB^2 = 2 \cdot AB^2
\]
\[
BC^2 = 2 \cdot 3^2 = 2 \cdot 9 = 18
\]
\[
BC = \sqrt{18} = 3\sqrt{2} \text{ cm}
\]

2. Tính cạnh AC:

Vì tam giác vuông đều có các cạnh đối diện góc $45^\circ$ bằng nhau:
\[
AC = AB = 3 \text{ cm}
\]

3. Tính góc B:

Góc $B$ trong tam giác vuông đều là $45^\circ$, vì tổng ba góc trong tam giác vuông là $180^\circ$, và góc vuông $A$ đã có $90^\circ$, do đó hai góc còn lại đều là $45^\circ$.

Kết luận:

- Cạnh BC: $3\sqrt{2}$ cm
- Cạnh AC: $3$ cm
- Góc B: $45^\circ$

...Xem thêm

Answer 2