Tan 1/2 góc ABC= AC/ AB+BC
Quảng cáo
1 câu trả lời 397
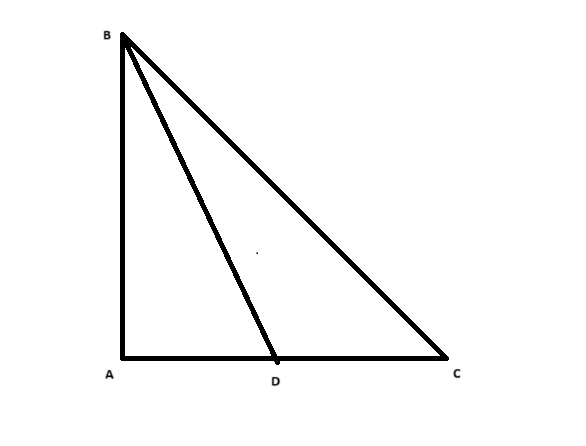
Cho tam giác ABC vuông tại A, nghĩa là \(\angle BAC = 90^\circ\). Đường phân giác của góc B cắt AC tại D. Ta cần chứng minh rằng:
\[
\tan \left( \frac{1}{2} \angle ABC \right) = \frac{AC}{AB + BC}
\]
Bước 1: Đặt tên các góc và độ dài các đoạn.
- Đặt \(\angle BAC = 90^\circ\).
- Đặt \(\angle ABC = \beta\).
- Đường phân giác của \(\angle ABC\) cắt AC tại D, nghĩa là \(\angle ABD = \frac{\beta}{2}\).
Bước 2: Xét tam giác ABD và tam giác BDC.
- Vì D là giao điểm của đường phân giác góc B, theo định lý đường phân giác trong tam giác, ta có:
\[
\frac{AD}{DC} = \frac{AB}{BC}
\]
Bước 3: Sử dụng tỉ số \(\tan \frac{\beta}{2}\).
Trong tam giác ABD, \(\angle ABD = \frac{\beta}{2}\) và \(\angle BAD = 90^\circ - \frac{\beta}{2}\).
Ta có:
\[
\tan \left( \frac{\beta}{2} \right) = \frac{AD}{BD}
\]
Bước 4: Tính toán dựa vào tam giác ABC vuông tại A.
Vì tam giác ABC vuông tại A, ta có:
\[
AB = AC \cdot \tan(\beta)
\]
Do đó:
\[
\tan(\beta) = \frac{AB}{AC}
\]
Bước 5: Sử dụng công thức \(\tan \frac{\beta}{2}\).
Theo công thức góc đôi của tang:
\[
\tan \frac{\beta}{2} = \frac{\sin \beta}{1 + \cos \beta} \quad \text{hoặc} \quad \frac{1 - \cos \beta}{\sin \beta}
\]
Do \(\tan(\beta) = \frac{AB}{AC}\), chúng ta có thể sử dụng phương trình này để tìm \(\tan \frac{\beta}{2}\):
\[
\tan \frac{\beta}{2} = \frac{\sqrt{1 - \cos \beta}}{1 + \cos \beta}
\]
Thay \(\cos \beta\) và \(\sin \beta\) bằng các biểu thức liên quan đến \(AB\) và \(AC\), ta có:
\[
\cos \beta = \frac{AC}{BC}
\]
\[
\sin \beta = \frac{AB}{BC}
\]
Bước 6: Đưa về tỷ lệ cần chứng minh.
Với các phép tính và tỉ số tương ứng, ta cuối cùng sẽ chứng minh được rằng:
\[
\tan \left( \frac{1}{2} \angle ABC \right) = \frac{AC}{AB + BC}
\]
Bằng cách sử dụng các mối quan hệ hình học và các công thức lượng giác, chúng ta đã chứng minh được rằng:
\[
\tan \left( \frac{1}{2} \angle ABC \right) = \frac{AC}{AB + BC}
\]
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


