**Bài a)**

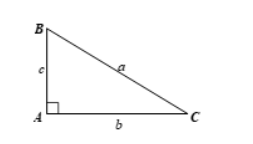
Xét tam giác \(\Delta ABC\) vuông tại \(A\):

- Cho biết \(a = 21\), \(b = 18\).

Theo định lý Pythagore, ta có:
\[ c = \sqrt{a^2 - b^2} = \sqrt{21^2 - 18^2} = \sqrt{441 - 324} = \sqrt{117} = \sqrt{3^2 \cdot 13} = 3\sqrt{13} \]

Theo định nghĩa tỉ số lượng giác sin, ta có:
\[ \sin B = \frac{b}{a} = \frac{18}{21} = \frac{6}{7} \]
T

ừ đó tìm được góc \(\hat{B}\):
\[ \hat{B} \approx \sin^{-1}\left(\frac{6}{7}\right) \approx 59^\circ \]

Theo định lý tổng ba góc của một tam giác, ta có:
\[ \hat{A} + \hat{B} + \hat{C} = 180^\circ \]

Do \(\hat{A} = 90^\circ\), suy ra:
\[ \hat{C} = 180^\circ - 90^\circ - \hat{B} \approx 180^\circ - 90^\circ - 59^\circ = 31^\circ \]

Vậy tam giác \(\Delta ABC\) có:
\[ \hat{A} = 90^\circ, \hat{B} \approx 59^\circ, \hat{C} \approx 31^\circ, a = 21, b = 18, c = 3\sqrt{13} \]

**Bài b)**

Xét tam giác \(\Delta ABC\) vuông tại \(A\):

- Cho biết \(\hat{C} = 30^\circ\), \(b = 10\).

Theo định lý tổng ba góc của một tam giác, ta có:
\[ \hat{A} + \hat{B} + \hat{C} = 180^\circ \]

Do \(\hat{A} = 90^\circ\), suy ra:
\[ \hat{B} = 90^\circ - \hat{C} = 90^\circ - 30^\circ = 60^\circ \]

Theo định nghĩa tỉ số lượng giác tan, ta có:
\[ AB = c = b \cdot \tan C = 10 \cdot \tan 30^\circ = 10 \cdot \frac{\sqrt{3}}{3} = \frac{10\sqrt{3}}{3} \]

Theo định nghĩa tỉ số lượng giác cos, ta có:
\[ AC = b = a \cdot \cos C \Rightarrow a = \frac{b}{\cos C} = \frac{10}{\cos 30^\circ} = \frac{10}{\frac{\sqrt{3}}{2}} = \frac{20}{\sqrt{3}} = \frac{20\sqrt{3}}{3} \]

Vậy tam giác \(\Delta ABC\) có:
\[ \hat{A} = 90^\circ, \hat{B} = 60^\circ, \hat{C} = 30^\circ, a = \frac{20\sqrt{3}}{3}, b = 10, c = \frac{10\sqrt{3}}{3} \]

**Bài c)**

Xét tam giác \(\Delta ABC\) vuông tại \(A\):

- Cho biết \(b = 3\), \(c = 5\).

Theo định lý Pythagore, ta có:
\[ a = \sqrt{b^2 + c^2} = \sqrt{3^2 + 5^2} = \sqrt{9 + 25} = \sqrt{34} \]

Theo định nghĩa tỉ số lượng giác tan, ta có:
\[ \tan B = \frac{b}{c} = \frac{3}{5} \]

Từ đó tìm được góc \(\hat{B}\):
\[ \hat{B} \approx \tan^{-1}\left(\frac{3}{5}\right) \approx 31^\circ \]

Theo định lý tổng ba góc của một tam giác, ta có:
\[ \hat{A} + \hat{B} + \hat{C} = 180^\circ \]

Do \(\hat{A} = 90^\circ\), suy ra:
\[ \hat{C} = 180^\circ - 90^\circ - \hat{B} \approx 180^\circ - 90^\circ - 31^\circ = 59^\circ \]

Vậy tam giác \(\Delta ABC\) có:
\[ \hat{A} = 90^\circ, \hat{B} \approx 31^\circ, \hat{C} \approx 59^\circ, a = \sqrt{34}, b = 3, c = 5 \]

*Bài a)**

Xét tam giác ΔABCΔ𝐴𝐵𝐶 vuông tại A𝐴:

- Cho biết a=21𝑎=21, b=18𝑏=18.

Theo định lý Pythagore, ta có:
c=√a2−b2=√212−182=√441−324=√117=√32⋅13=3√13𝑐=𝑎2−𝑏2=212−182=441−324=117=32⋅13=313

Theo định nghĩa tỉ số lượng giác sin, ta có:
sinB=ba=1821=67sin⁡𝐵=𝑏𝑎=1821=67
T

ừ đó tìm được góc ^B𝐵^:
^B≈sin−1(67)≈59∘𝐵^≈sin−1⁡(67)≈59∘

Theo định lý tổng ba góc của một tam giác, ta có:
^A+^B+^C=180∘𝐴^+𝐵^+𝐶^=180∘

Do ^A=90∘𝐴^=90∘, suy ra:
^C=180∘−90∘−^B≈180∘−90∘−59∘=31∘𝐶^=180∘−90∘−𝐵^≈180∘−90∘−59∘=31∘

Vậy tam giác ΔABCΔ𝐴𝐵𝐶 có:
^A=90∘,^B≈59∘,^C≈31∘,a=21,b=18,c=3√13𝐴^=90∘,𝐵^≈59∘,𝐶^≈31∘,𝑎=21,𝑏=18,𝑐=313

**Bài b)**

Xét tam giác ΔABCΔ𝐴𝐵𝐶 vuông tại A𝐴:

- Cho biết ^C=30∘𝐶^=30∘, b=10𝑏=10.

Theo định lý tổng ba góc của một tam giác, ta có:
^A+^B+^C=180∘𝐴^+𝐵^+𝐶^=180∘

Do ^A=90∘𝐴^=90∘, suy ra:
^B=90∘−^C=90∘−30∘=60∘𝐵^=90∘−𝐶^=90∘−30∘=60∘

Theo định nghĩa tỉ số lượng giác tan, ta có:
AB=c=b⋅tanC=10⋅tan30∘=10⋅√33=10√33𝐴𝐵=𝑐=𝑏⋅tan⁡𝐶=10⋅tan⁡30∘=10⋅33=1033

Theo định nghĩa tỉ số lượng giác cos, ta có:
AC=b=a⋅cosC⇒a=bcosC=10cos30∘=10√32=20√3=20√33𝐴𝐶=𝑏=𝑎⋅cos⁡𝐶⇒𝑎=𝑏cos⁡𝐶=10cos⁡30∘=1032=203=2033

Vậy tam giác ΔABCΔ𝐴𝐵𝐶 có:
^A=90∘,^B=60∘,^C=30∘,a=20√33,b=10,c=10√33𝐴^=90∘,𝐵^=60∘,𝐶^=30∘,𝑎=2033,𝑏=10,𝑐=1033

**Bài c)**

Xét tam giác ΔABCΔ𝐴𝐵𝐶 vuông tại A𝐴:

- Cho biết b=3𝑏=3, c=5𝑐=5.

Theo định lý Pythagore, ta có:
a=√b2+c2=√32+52=√9+25=√34𝑎=𝑏2+𝑐2=32+52=9+25=34

Theo định nghĩa tỉ số lượng giác tan, ta có:
tanB=bc=35tan⁡𝐵=𝑏𝑐=35

Từ đó tìm được góc ^B𝐵^:
^B≈tan−1(35)≈31∘𝐵^≈tan−1⁡(35)≈31∘

Theo định lý tổng ba góc của một tam giác, ta có:
^A+^B+^C=180∘𝐴^+𝐵^+𝐶^=180∘

Do ^A=90∘𝐴^=90∘, suy ra:
^C=180∘−90∘−^B≈180∘−90∘−31∘=59∘𝐶^=180∘−90∘−𝐵^≈180∘−90∘−31∘=59∘

Vậy tam giác ΔABCΔ𝐴𝐵𝐶 có:
^A=90∘,^B≈31∘,^C≈59∘,a=√34,b=3,c=5