Cho tam giác ABC vuông tại A,đường caoAH.BiếtBH=8cm,CH=2cm.Độ dài AH là
Quảng cáo
2 câu trả lời 154
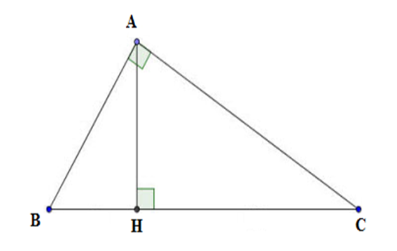
Trong tam giác vuông \(ABC\) vuông tại \(A\), đường cao \(AH\) hạ từ \(A\) xuống cạnh \(BC\). Được biết \(BH = 8 \text{ cm}\) và \(CH = 2 \text{ cm}\).
Theo tính chất của tam giác vuông, ta có:
\[ BH \cdot CH = AH^2 \]
Thay các giá trị đã biết vào phương trình trên:
\[ 8 \cdot 2 = AH^2 \]
Tính tích của \(BH\) và \(CH\):
\[ 16 = AH^2 \]
Giải phương trình để tìm \(AH\):
\[ AH = \sqrt{16} \]
Do \(AH\) là độ dài nên ta chỉ lấy giá trị dương của căn bậc hai:
\[ AH = 4 \text{ cm} \]
Vậy độ dài của \(AH\) là \(4 \text{ cm}\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103771
Đã trả lời bởi chuyên gia
103771 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68984
Đã trả lời bởi chuyên gia
68984 -
 Đã trả lời bởi chuyên gia
56864
Đã trả lời bởi chuyên gia
56864 -
 Đã trả lời bởi chuyên gia
47673
Đã trả lời bởi chuyên gia
47673 -
 Đã trả lời bởi chuyên gia
44539
Đã trả lời bởi chuyên gia
44539 -
 Đã trả lời bởi chuyên gia
36974
Đã trả lời bởi chuyên gia
36974 -
 Đã trả lời bởi chuyên gia
35600
Đã trả lời bởi chuyên gia
35600
Gửi báo cáo thành công!



