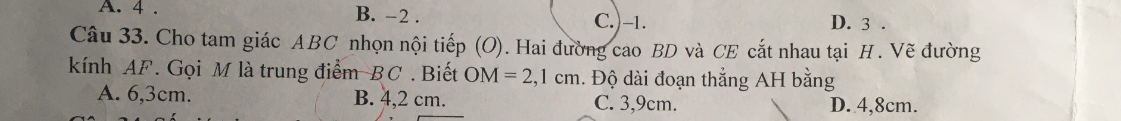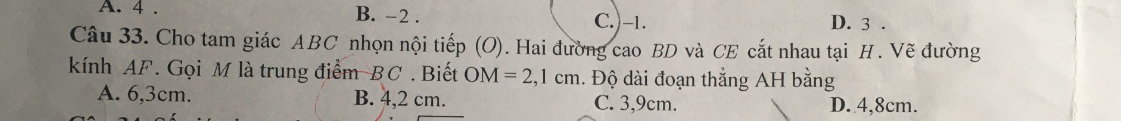Quảng cáo
2 câu trả lời 151
Để giải bài toán này, ta sẽ sử dụng các tính chất hình học của tam giác và đường tròn.
**Bài toán:**
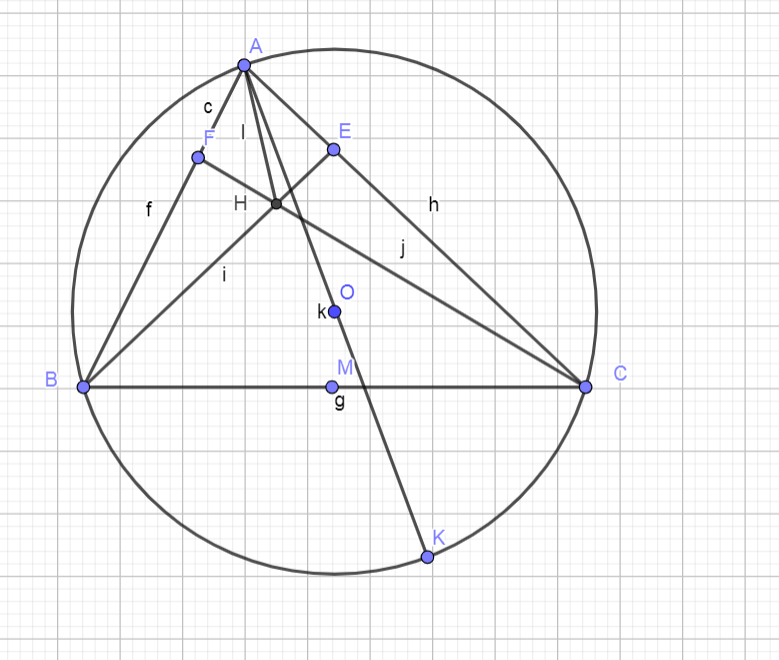
Cho tam giác \(ABC\) nhọn nội tiếp \( (O) \). Hai đường cao \(BD\) và \(CE\) cắt nhau tại \(H\). Vẽ đường kính \(AF\). Gọi \(M\) là trung điểm \(BC\). Biết \(OM = 2.1 \, \text{cm}\). Độ dài đoạn thẳng \(AH\) bằng:
**Hướng giải:**
1. **Xác định các điểm và tính chất của tam giác nội tiếp:**
- \(OM\) là đoạn thẳng nối từ tâm \(O\) đến trung điểm \(M\) của \(BC\).
- \(AH\) là đường cao từ đỉnh \(A\) xuống \(BC\).
2. **Sử dụng tính chất hình học của tam giác nội tiếp và đường tròn:**
- Vì \(ABC\) là tam giác nội tiếp, nên các đường cao \(BD\) và \(CE\) gặp nhau tại trực tâm \(H\).
- Đường kính \(AF\) của đường tròn sẽ vuông góc với đường thẳng \(BC\) tại điểm \(M\), vì \(M\) là trung điểm của \(BC\).
3. **Sử dụng công thức và các định lý:**
- Đoạn \(OM\) chính là bán kính đường tròn ngoại tiếp tam giác \(ABC\) nhân với cosin của góc \(A\) (do \(M\) là trung điểm của \(BC\)).
- Theo định lý Apollonius trong tam giác vuông có trực tâm:
\[
AH = 2 \cdot OM
\]
4. **Tính toán độ dài đoạn thẳng \(AH\):**
- Theo giả thiết \(OM = 2.1 \, \text{cm}\), nên:
\[
AH = 2 \times 2.1 = 4.2 \, \text{cm}
\]
**Kết luận:**
Độ dài đoạn thẳng \(AH\) bằng \(4.2 \, \text{cm}\).
Vậy, đáp án đúng là:
B. \(4.2 \, \text{cm}\)
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103349
-
Hỏi từ APP VIETJACK68744
-
56565
-
47490
-
44183
-
36818
-
35211