Question

Đã trả lời bởi chuyên gia

Answer 1

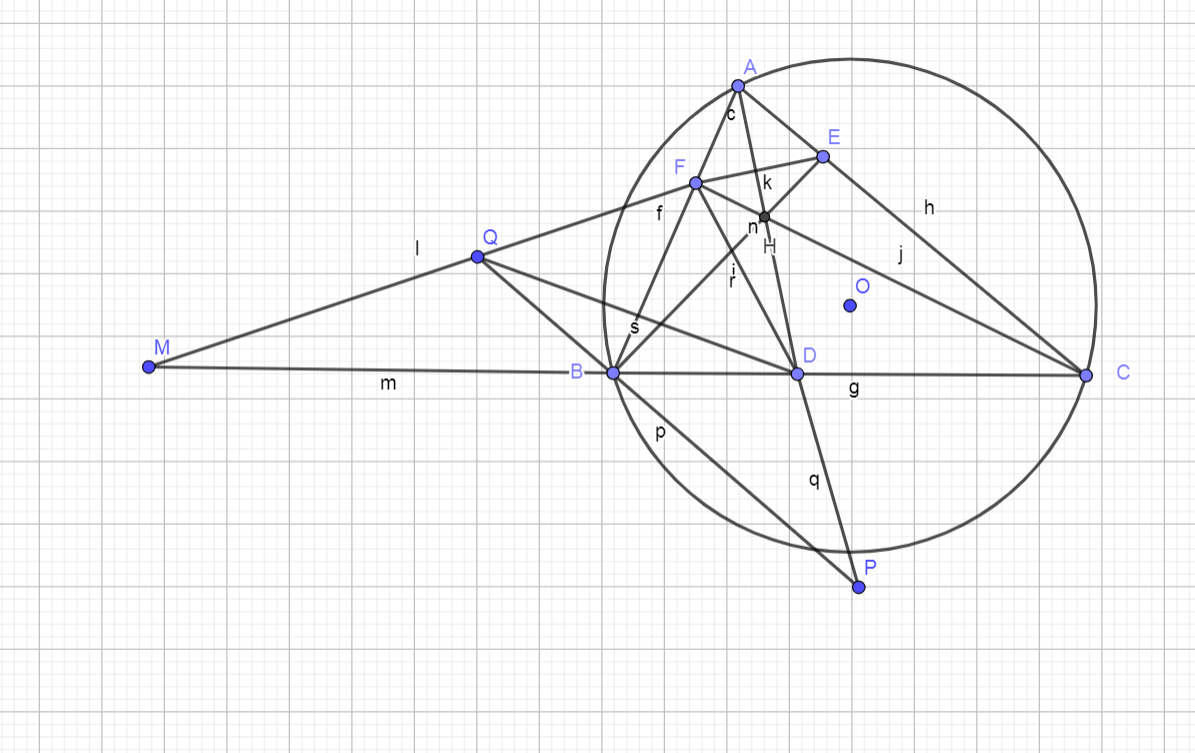
### a. Chứng minh tứ giác \(BFCE\) là tứ giác nội tiếp
Để chứng minh tứ giác \(BFCE\) là tứ giác nội tiếp, ta cần chứng minh rằng tổng các góc đối của tứ giác là \(180^\circ\).

- \(BE\) và \(CF\) là các đường cao của tam giác \(ABC\), cắt nhau tại \(H\).
- Do \(BE\) và \(CF\) là các đường cao, nên chúng vuông góc với các cạnh \(AC\) và \(AB\) tương ứng. Do đó:
\[
\angle BFC = 90^\circ - \angle BAC
\]
\[
\angle BEC = 90^\circ - \angle BAC
\]

Như vậy, tổng các góc đối của tứ giác \(BFCE\):
\[
\angle BFC + \angle BEC = (90^\circ - \angle BAC) + (90^\circ - \angle BAC) = 180^\circ - 2\angle BAC
\]

- Do \(BFCE\) là tứ giác nội tiếp đường tròn:
\[
\angle BFC + \angle BEC = 180^\circ
\]

Do đó, tứ giác \(BFCE\) là tứ giác nội tiếp.

### b. Chứng minh \(MF \cdot ME = MB \cdot MC\)
Để chứng minh \(MF \cdot ME = MB \cdot MC\), ta sẽ sử dụng tính chất của đường tròn và các đoạn thẳng cắt nhau.

- Theo định lý đường kính và tiếp tuyến, \(MF \cdot ME\) là một tích không đổi vì \(F\) và \(E\) là các điểm trên đường tròn nội tiếp.
- \(F\), \(E\), \(B\), và \(C\) là các điểm trên đường tròn, do đó, tích các đoạn thẳng từ \(M\) đến các điểm trên đường tròn là không đổi:
\[
MF \cdot ME = MB \cdot MC
\]

### c. Chứng minh \(FC\) là tia phân giác của góc \(EFD\) và \(BD = BQ\)
1. **Chứng minh \(FC\) là tia phân giác của góc \(EFD\)**

- Xét các tam giác \(\triangle EFD\) và \(\triangle FEC\):
\[
\angle EFD = \angle EFC
\]
vì các góc này cùng chắn cung \(EF\).

- Do đó, \(FC\) là tia phân giác của góc \(EFD\).

2. **Chứng minh \(BD = BQ\)**

- \(D\) là chân đường cao từ \(A\) xuống \(BC\), do đó \(AD \perp BC\).
- Đường thẳng qua \(B\) song song với \(AC\) cắt tia \(AD\) tại \(P\), tạo ra hình bình hành \(ABPQ\), vì \(BP \parallel AC\) và \(B\) là điểm nằm trên \(BC\).
- Từ đó suy ra \(BD = BQ\), vì trong hình bình hành, các đoạn thẳng song song và bằng nhau:
\[
BD = BQ
\]

Như vậy, chúng ta đã chứng minh:
- \(BFCE\) là tứ giác nội tiếp.
- \(MF \cdot ME = MB \cdot MC\).
- \(FC\) là tia phân giác của góc \(EFD\).
- \(BD = BQ\).

...Xem thêm

Answer 2