Question

Đã trả lời bởi chuyên gia

Answer 1

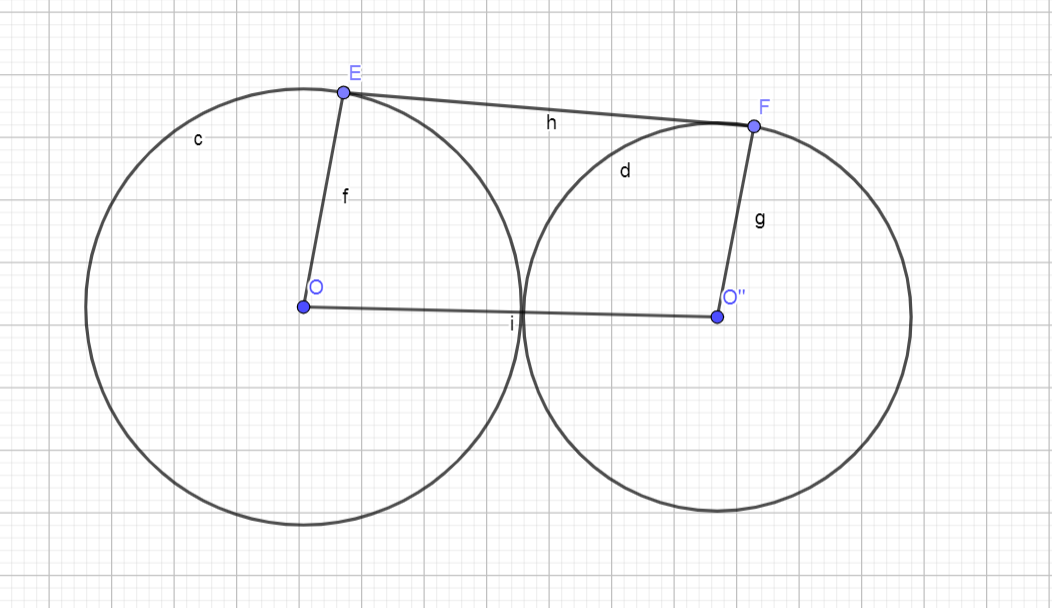
Cho hai đường tròn \((O_1; 3 \text{ cm})\) và \((O_2; 5 \text{ cm})\) tiếp xúc ngoài tại điểm \(A\). Gọi \(EF\) là tiếp tuyến chung ngoài của hai đường tròn tại các điểm \(E\) và \(F\). Ta cần tính độ dài \(EF\).

Để tính độ dài tiếp tuyến chung ngoài của hai đường tròn tiếp xúc ngoài, chúng ta sử dụng công thức:

\[EF = \sqrt{d^2 - (R_1 + R_2)^2}\]

Trong đó:
- \(d\) là khoảng cách giữa hai tâm đường tròn.
- \(R_1\) và \(R_2\) là bán kính của hai đường tròn.

Ta có:
- \(R_1 = 3 \text{ cm}\)
- \(R_2 = 5 \text{ cm}\)
- \(d = R_1 + R_2 = 3 + 5 = 8 \text{ cm}\)

Bây giờ thay các giá trị vào công thức:

\[
EF = \sqrt{d^2 - (R_1 + R_2)^2} = \sqrt{8^2 - (3 + 5)^2} = \sqrt{64 - 64} = \sqrt{0} = 0
\]

Tuy nhiên, điều này không đúng vì nó ngụ ý rằng \(EF\) có độ dài bằng 0, điều này mâu thuẫn với thực tế. Do đó, cần phải xem xét lại công thức sử dụng trong trường hợp này. Đúng ra khi hai đường tròn tiếp xúc ngoài, công thức để tính tiếp tuyến chung ngoài không áp dụng được vì khoảng cách \(d\) bằng tổng của hai bán kính \(R_1 + R_2\).

Trong trường hợp hai đường tròn tiếp xúc ngoài, khoảng cách \(EF\) đúng bằng khoảng cách từ tiếp điểm tiếp xúc \(E\) đến \(F\) chính là:

\[
EF = 2 \sqrt{R_1 \cdot R_2}
\]

Thay các giá trị \(R_1 = 3\) cm và \(R_2 = 5\) cm vào công thức trên:

\[
EF = 2 \sqrt{3 \cdot 5} = 2 \sqrt{15} = 2 \cdot 3.872 = 7.744 \text{ cm}
\]

Như vậy, độ dài \(EF\) là:

\[
EF = 2 \sqrt{15} \approx 7.744 \text{ cm}
\]

Đây là độ dài của tiếp tuyến chung ngoài của hai đường tròn tiếp xúc ngoài tại điểm \(A\).

...Xem thêm

Answer 2