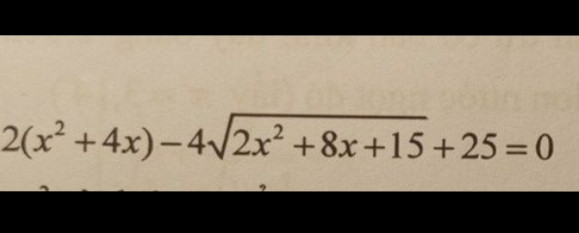Question

Đã trả lời bởi chuyên gia

Answer 1

Để giải phương trình \(2(x^2 + 4x) - 4\sqrt{2x^2 + 8x + 15} + 25 = 0\), chúng ta sẽ thực hiện các bước chi tiết sau:

1. **Đơn giản hóa phương trình:**
\(2(x^2 + 4x) - 4\sqrt{2x^2 + 8x + 15} + 25 = 0\)

2. **Biến đổi các biểu thức:**
\[2x^2 + 8x - 4\sqrt{2x^2 + 8x + 15} + 25 = 0\]

3. **Đặt \(u = 2x^2 + 8x\):**
Ta có:
\[u - 4\sqrt{u + 15} + 25 = 0\]

4. **Chuyển vế và phân tích:**
\[u + 25 = 4\sqrt{u + 15}\]
Bình phương cả hai vế để loại bỏ căn:
\[(u + 25)^2 = (4\sqrt{u + 15})^2\]
\[u^2 + 50u + 625 = 16(u + 15)\]
\[u^2 + 50u + 625 = 16u + 240\]
\[u^2 + 50u + 625 - 16u - 240 = 0\]
\[u^2 + 34u + 385 = 0\]

5. **Giải phương trình bậc hai:**
Áp dụng công thức nghiệm:
\[u = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
với \(a = 1\), \(b = 34\), \(c = 385\):
\[u = \frac{-34 \pm \sqrt{34^2 - 4 \cdot 1 \cdot 385}}{2 \cdot 1}\]
\[u = \frac{-34 \pm \sqrt{1156 - 1540}}{2}\]
\[u = \frac{-34 \pm \sqrt{-384}}{2}\]
\[u = \frac{-34 \pm 16i\sqrt{6}}{2}\]
\[u = -17 \pm 8i\sqrt{6}\]

6. **Tìm \(x\):**
Ta có \(u = 2x^2 + 8x\). Tuy nhiên, vì \(u\) có phần ảo, điều này cho thấy không có nghiệm thực cho phương trình ban đầu trong tập số thực.

Kết luận: Phương trình \(2(x^2 + 4x) - 4\sqrt{2x^2 + 8x + 15} + 25 = 0\) không có nghiệm thực.

...Xem thêm

Answer 2