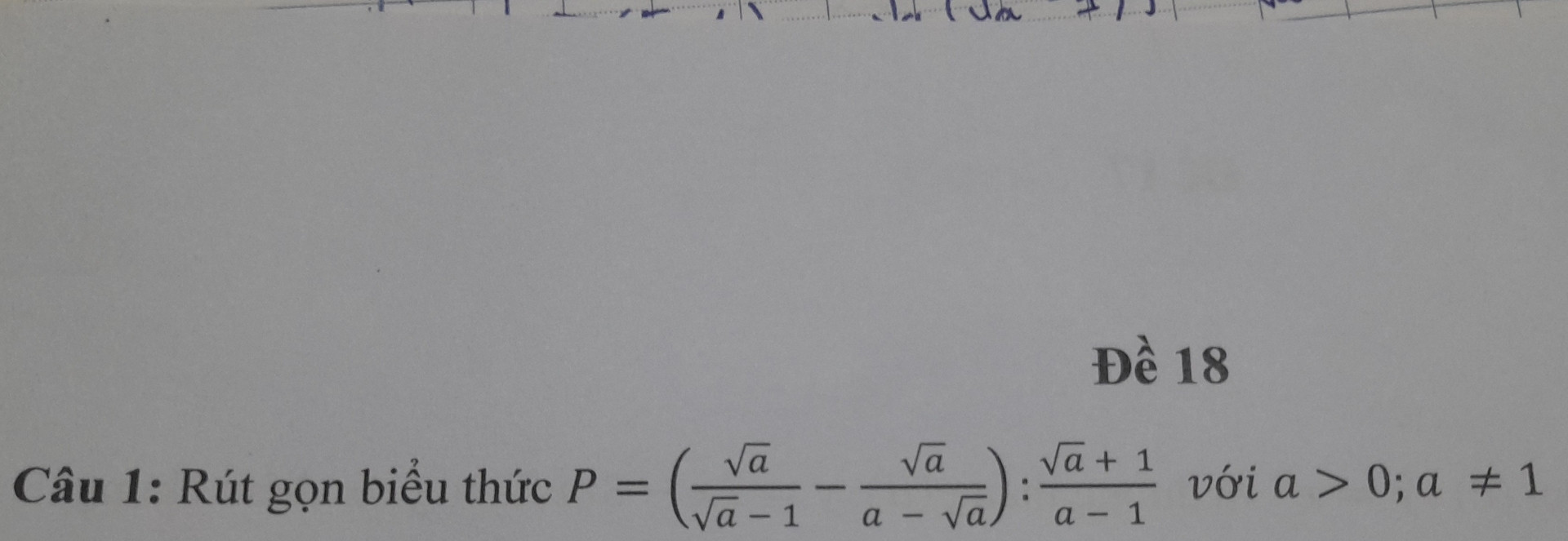Rút gọn biểu thức P =
Quảng cáo
3 câu trả lời 258
Để rút gọn biểu thức \( P = \frac{\sqrt{a}}{\sqrt{a} - 1} - \frac{\sqrt{a}}{a - \sqrt{a}} : \frac{\sqrt{a} + 1}{a - 1} \), ta thực hiện các bước sau:
1. Tìm chung mẫu số cho phần tử phân số đầu tiên và phần tử phân số thứ hai của biểu thức.
2. Thực hiện phép tính chia các phân số.
3. Rút gọn kết quả nếu có thể.
Bước 1: Tìm chung mẫu số
Để tìm chung mẫu số, ta nhân mỗi phần tử và mẫu số của mỗi phần tử để có một mẫu số chung:
\[ \sqrt{a}(\sqrt{a} + 1)(a - \sqrt{a}) \]
Bước 2: Thực hiện phép tính
Thay thế các phần tử trong biểu thức với mẫu số chung:
\[ P = \frac{\sqrt{a}(\sqrt{a} + 1)(a - \sqrt{a})}{\sqrt{a} - 1} - \frac{\sqrt{a}(\sqrt{a} + 1)(a - \sqrt{a})}{a - \sqrt{a}} : \frac{\sqrt{a}(\sqrt{a} + 1)}{a - 1} \]
Bước 3: Rút gọn
Rút gọn biểu thức:
\[ P = \frac{\sqrt{a}(\sqrt{a} + 1)(a - \sqrt{a})}{\sqrt{a} - 1} - \frac{\sqrt{a}(\sqrt{a} + 1)(a - \sqrt{a})}{a - \sqrt{a}} \times \frac{a - 1}{\sqrt{a}(\sqrt{a} + 1)} \]
\[ P = \frac{\sqrt{a}(\sqrt{a} + 1)(a - \sqrt{a})}{\sqrt{a} - 1} - \frac{a - 1}{a - \sqrt{a}} \]
\[ P = \frac{\sqrt{a}(\sqrt{a} + 1)(a - \sqrt{a})}{\sqrt{a} - 1} - \frac{\sqrt{a} - 1}{a - \sqrt{a}} \]
Đây là biểu thức rút gọn của \( P \).
$P = \frac{a - \sqrt{a} - (\sqrt{a}(\sqrt{a} - 1))}{a - \sqrt{a}} : \frac{\sqrt{a} + 1}{a - 1}$
$P = \frac{a - \sqrt{a} - (a - \sqrt{a})}{a - \sqrt{a}} : \frac{\sqrt{a} + 1}{a - 1}$
$P = \frac{0}{a - \sqrt{a}} : \frac{\sqrt{a} + 1}{a - 1}$
$P = 0 : \frac{\sqrt{a} + 1}{a - 1}$
$P = 0$
=> Vậy biểu thức P sau khi rút gọn sẽ bằng 0 với mọi $a > 0$ và $a \neq 1$.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274