Bảo MinhLê Cao
Hỏi từ APP VIETJACK
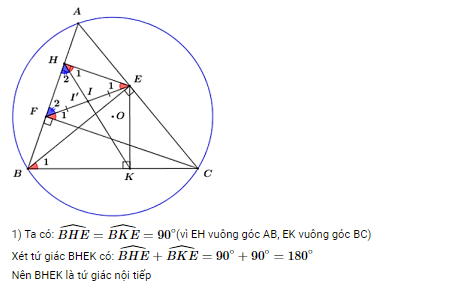
IV. (3,0 điểm) Cho tam giác ABC có ba góc nhọn và đường cao BE, Gọi H và K lần lượt là chân đường cao
m thứ hai x kẻ từ E đến các đường thẳng AB và BC.
1) Chứng minh BHEK là tứ giác nội tiếp và HKE = AEH.
1, 1 thẳng hà
2) Gọi F là chân đường vuông góc kẻ từ C đến AB, G là giao điểm của BE và CF; AG cắt BC tại Q; O là trung điểm của BC. Chứng minh BHBA = BK.BC và bốn điểm E, F, Q, O cùng thuộc một đường tròn.
3) Gọi P là trung điểm của AG; 1 là trung điểm của EF .
a) Chứng minh PF là tiếp tuyến của đường tròn đường kính BC.
b) Chứng minh ba điểm H,I,K là ba điểm thẳng hàng.
m thứ hai x kẻ từ E đến các đường thẳng AB và BC.
1) Chứng minh BHEK là tứ giác nội tiếp và HKE = AEH.
1, 1 thẳng hà
2) Gọi F là chân đường vuông góc kẻ từ C đến AB, G là giao điểm của BE và CF; AG cắt BC tại Q; O là trung điểm của BC. Chứng minh BHBA = BK.BC và bốn điểm E, F, Q, O cùng thuộc một đường tròn.
3) Gọi P là trung điểm của AG; 1 là trung điểm của EF .
a) Chứng minh PF là tiếp tuyến của đường tròn đường kính BC.
b) Chứng minh ba điểm H,I,K là ba điểm thẳng hàng.
Quảng cáo
1 câu trả lời 711
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387
Gửi báo cáo thành công!