Quảng cáo
3 câu trả lời 1748
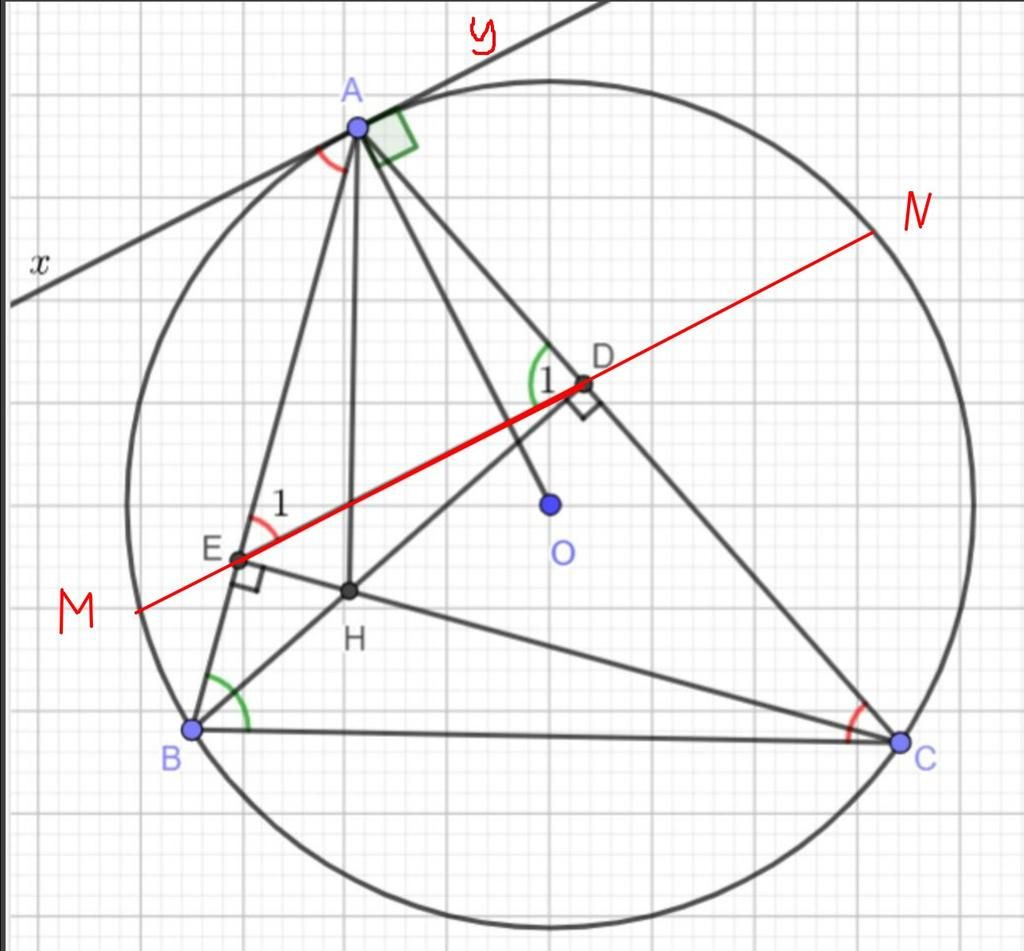
a) Chứng minh: tứ giác ADHE nội tiếp.
- Ta có tam giác ABC nội tiếp đường tròn (O), do đó các góc ở đỉnh của tam giác ABC bằng góc ở tâm của đường tròn (O).
- Góc ADB = 90 độ (vì BD là đường cao của tam giác ABC).
- Góc AEB = 90 độ (vì CE là đường cao của tam giác ABC).
- Vậy tứ giác ADHE là tứ giác nội tiếp.
b) Gọi M, N là giao điểm của DE với đường tròn, xy là tiếp tuyến của đường tròn (O) tại A.
- Theo tính chất của tiếp tuyến và dây cung, ta có: góc MAN = góc MNA = góc A.
- Vậy ta có tứ giác AMAN là tứ giác hình thang.
- Do đó, góc MAN = góc MNA = góc A = góc HDE (do tứ giác ADHE nội tiếp).
- Vậy ta có tứ giác HDE cũng là tứ giác hình thang.
a: góc ADH+góc AEH=180 độ
=>ADHE nội tiếp
b; góc xAC=góc ABC
=>góc xAC=góc ADE
=>xy//DE
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387