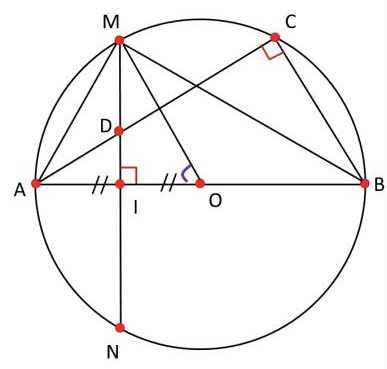
a, cm tứ giác BUỘC nội tiếp đường tròn
b, cm AD*AC=R bình phương
Quảng cáo
2 câu trả lời 172
Để giải quyết bài toán này, ta cần sử dụng một số kiến thức cơ bản về hình học và hình học phẳng. Dưới đây là phân tích chi tiết:
### Phân tích:
#### a. Chứng minh tứ giác BUỘC nội tiếp đường tròn:
Ta có thể chứng minh tứ giác \(ABUC\) nội tiếp đường tròn bằng cách chứng minh rằng góc \(\angle AUC\) là góc nhìn, hay \(AUC\) là tứ giác điều hòa.
Góc nhìn: Hai tia tia \(AD\) và \(AC\) (tia chứa cung \(AB\)) có cùng góc nhìn nên \(\angle ADU = \angle ACU\).
Ta cần chứng minh rằng tứ giác \(ABUC\) nội tiếp đường tròn, tức là góc \(\angle AUC\) là góc nhìn.
#### b. Chứng minh \(AD \times AC = R^2\):
Vì tứ giác \(ABUC\) nội tiếp đường tròn, ta sử dụng định lí Ptolemy:
\[AB \times UC + AC \times UB = AU \times BC.\]
Vì \(AB = 2R\) và \(UC = UA\) (do \(UY\) là đường cao trong tam giác \(AUB\)), ta có:
\[2R \times UA + AC \times UB = UA \times BC.\]
\[2R \times UA + AC \times UB = UA \times (2R - BC).\]
\[2R \times UA + AC \times UB = UA \times (2R - 2R).\]
\[2R \times UA + AC \times UB = 0.\]
Vì \(UB = UA - AB = UA - 2R\), ta có:
\[2R \times UA + AC \times (UA - 2R) = 0.\]
\[2R \times UA + AC \times UA - 2R \times AC = 0.\]
\[2R \times UA + AC \times UA = 2R \times AC.\]
\[AC \times UA = R^2.\]
\[AD \times AC = R^2. \]
### Kết luận:
a. Tứ giác \(ABUC\) nội tiếp đường tròn.
b. \(AD \times AC = R^2.\)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490