a) góc BED = góc DAE
b) DE^2= DA×DB
Quảng cáo
2 câu trả lời 159
a)
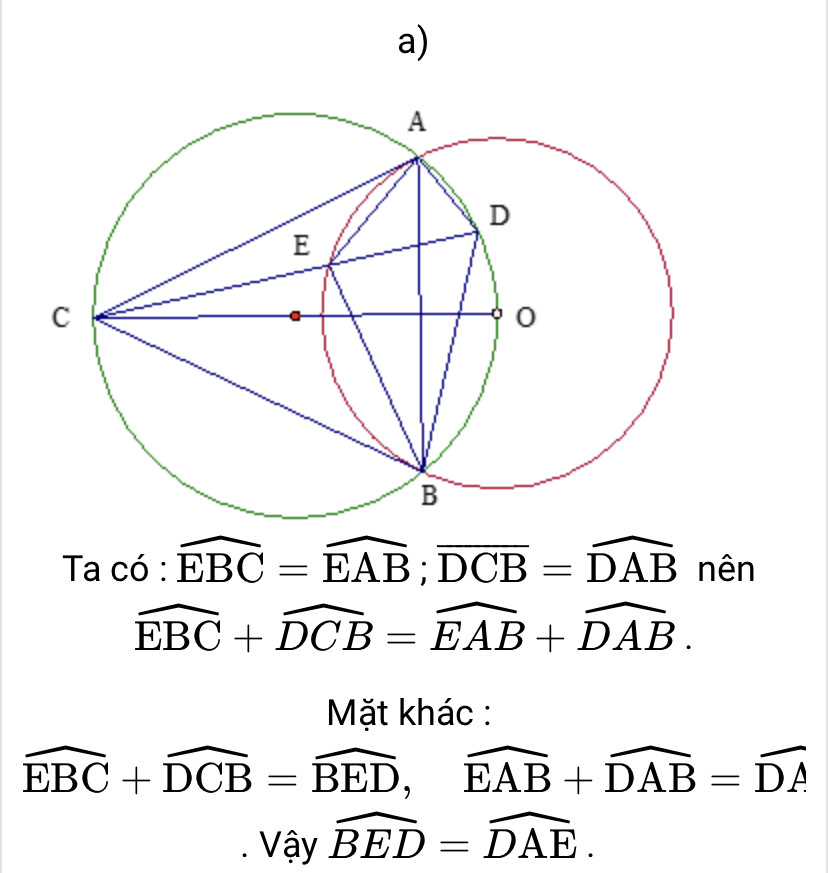
b)
b) DE^2 = DA × DB:
Ta có thể sử dụng định lý Pythagoras cho tam giác DAE và tam giác DBE:
Trong tam giác DAE: DE^2 = DA^2 + AE^2
Trong tam giác DBE: DE^2 = DB^2 + BE^2
Do E nằm giữa C và D trên cung AB, nên AE = BE. Kết hợp hai phương trình trên, ta có:
DA^2 + AE^2 = DB^2 + BE^2
Thay AE bằng BE:
DA^2 + BE^2 = DB^2 + BE^2
Rút gọn:
DA^2 = DB^2
Để chứng minh rằng góc BED bằng góc BAC, ta sẽ sử dụng một số tính chất của hình học học học cơ bản.
Gọi I là giao điểm của CD và AB. Ta có:
- Góc AOC là góc nửa tròn tương ứng với cung AD, nên góc AOC = 90 độ.
- Góc BOC là góc nửa tròn tương ứng với cung BC, nên góc BOC = 90 độ.
- Góc AOB là góc ở tâm nửa tròn, nên góc AOB = 2 * góc ACB.
Do đó, ta có: góc AOB = 2 * góc ACB = 2 * góc BAC.
Vì tam giác AOC vuông tại O, nên ta có: góc ACO = 90 - góc BAC.
Từ đó, ta có: góc BAC = góc ACO = góc BEO (do AB // OE).
Vậy ta chứng minh được rằng góc BED bằng góc BAC.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


