Cho đường tròn tâm O có dây BC cố định khác đường kính. Lấy điểm A bất kỳ trên cung lớn BC sao
cho tam giác ABC nhọn và AB < AC. Kẻ đường cao AE, CF của tam giác ABC. Kẻ đường kính AD của (O). Gọi N là
hình chiếu vuông góc của C trên AD.
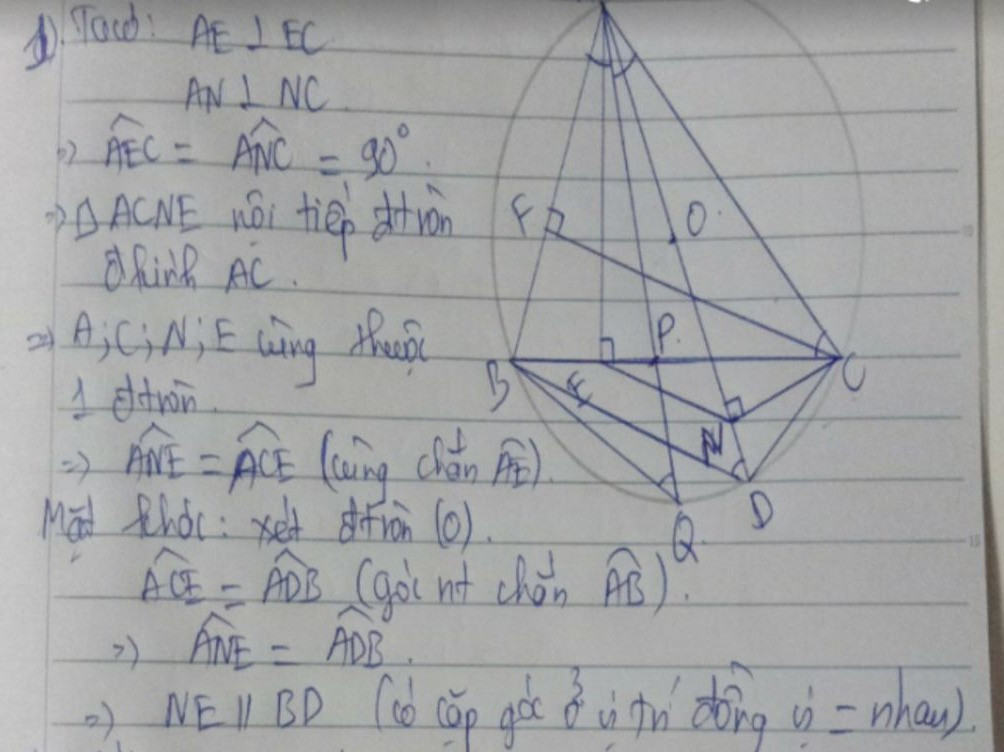
a) Chứng minh bốn điểm A, E, N, C cùng thuộc đường tròn đường kính AC.
b) Chứng minh EN song song với BD.
c) Chứng minh rằng khi điểm A di động trên cung lớn BC và thỏa mãn yêu cầu đầu bài thì đường thẳng NF luôn đi
qua một điểm cố định.
cho tam giác ABC nhọn và AB < AC. Kẻ đường cao AE, CF của tam giác ABC. Kẻ đường kính AD của (O). Gọi N là
hình chiếu vuông góc của C trên AD.
a) Chứng minh bốn điểm A, E, N, C cùng thuộc đường tròn đường kính AC.
b) Chứng minh EN song song với BD.
c) Chứng minh rằng khi điểm A di động trên cung lớn BC và thỏa mãn yêu cầu đầu bài thì đường thẳng NF luôn đi
qua một điểm cố định.
Quảng cáo
2 câu trả lời 3518
a)
Xét tứ giác AENC có:
Mà 2 đỉnh E và N kề nhau cùng nhìn cạnh AC dưới 1 góc vuông
⇒ Tứ giác AENC nội tiếp
⇒ Bốn điểm A, E, N, C cùng thuộc một đường tròn
b)
Ta có:
(2 góc nội tiếp cùng chắn cung DC)
hay
Ta lại có:
(2 góc nội tiếp cùng chắn cung NC do tứ giác AENC nội tiếp)
⇒ EN//BD (Do 2 góc ở vị trí đồng vị)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490
Gửi báo cáo thành công!