a) Chứng minh ED = EF . EG.
Quảng cáo
4 câu trả lời 1104
a) Để chứng minh ED = EF . EG, ta sử dụng tính chất của hình chữ nhật và đường cao.
Vì ABCD là hình bình hành, nên ta có AD || BC và AB = CD.
Khi đó, ta có các tam giác ABD và BCD là hai tam giác tương đồng (tam giác cân). Do đó, góc ADB = góc BDC.
Vì E, F, G lần lượt là hình chiếu vuông góc của D trên các đường thẳng AC, AB, BC, nên ta có:
ED || AB và EF || BC
Do góc ADB = góc BDC, ta có:
góc ADB = góc BDC = góc DEF (góc nội tại tương đồng)
Tương tự, ta có:
góc BDC = góc ADB = góc EGF (góc nội tại tương đồng)
Vậy, ta đã chứng minh được ED = EF . EG.
Câu 4:
a/
- Xét tứ giác EDGC là tứ giác nội tiếp ( )
nên (cùng chắn cung ED)
mà ( cùng phụ với )
=> (1)
- Xét tứ giác AFDE là tứ giác nội tiếp nên
Lại có tứ giác EDGC nội tiếp nên
mà (AD // BC) và (AB//CD)
=> (2)
Từ (1) và (2) => 1 đồng dạng 2 (gg)
=> 3 => 4 (đpcm)
b/ O, E, F, G cùng thuộc một đường tròn
Xét 5 vuông tại F có FO là đường trung tuyến ứng với cạnh huyền BD (vì OD = OB theo t/c hình bình hành) => OF = BD/2 = OD = OB
=> OF = OD => Tam giác OFD cân tại O
=> 6 => 7
Mà FBGD là tứ giác nội tiếp => 8 hay 9
=> 0
Lại có ECGD là tứ giác nội tiếp => 1
=> 2 hay 3
=> Tứ giác OEFG là tứ giác nội tiếp => 4 điểm cùng thuộc một đường tròn (đpcm)
c/ Gọi H là giao điểm của FG và AC. Chưng minh 4
Xét 5 vuông tại G có GO là đường trung tuyến ứng với cạnh huyền BD:
=> GO = 1/2BD = OD = OB
Mà OD = OF (cm b) => OG = OF => 6 cân tại O
=> 7
mà 8 (2 góc kề bù); tứ giác OEFG nội tiếp nên 9
=> 0 và 1 chung => 2 đồng dạng 3 (gg)
=> 4 => 5
mà OF = OD => 6 và 7chung
=> 8 đồng dạng 9 (cgc)
=> 0
=> 4 (đpcm)
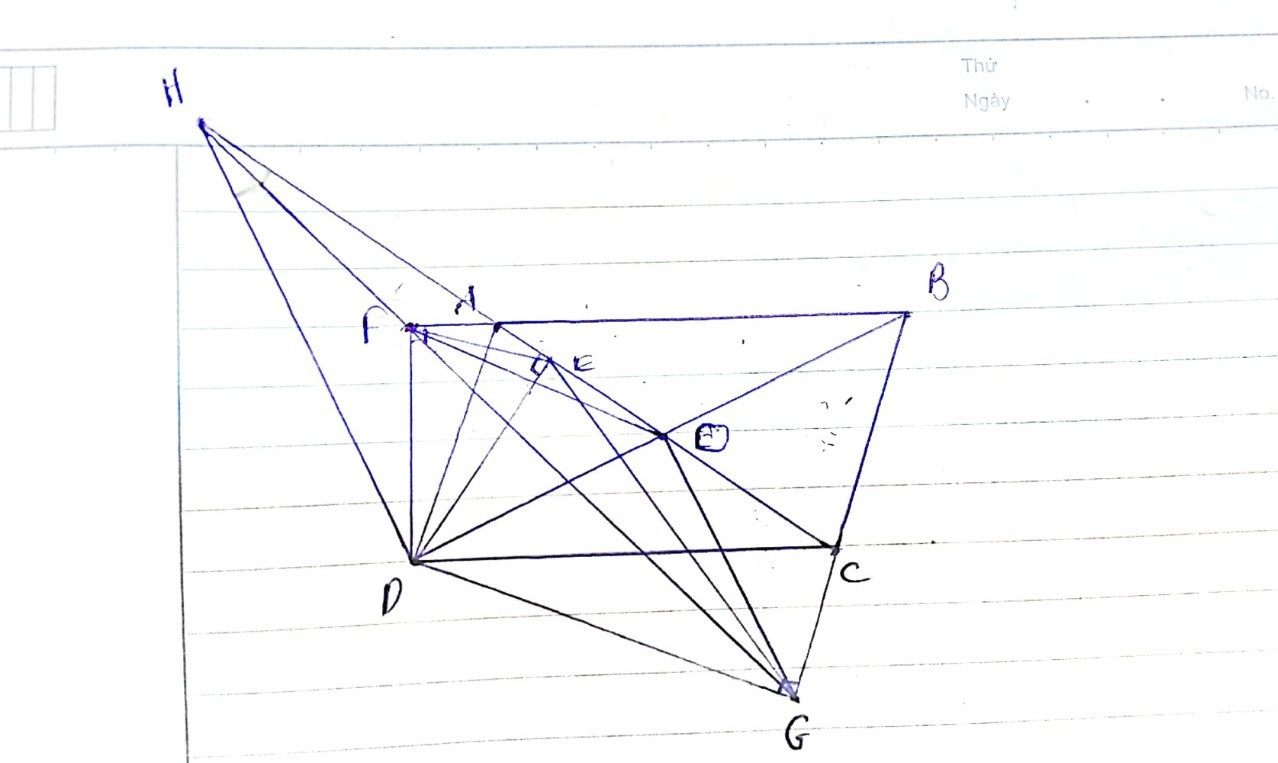
Đề thi CSP đợt 3 năm nay hả bạn? Đầy đủ câu hình như này đúng không?

Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


