a) Chứng minh tam giác MAB đều.
b) Tính độ dài cạnh AM.
c) Tia AO cắt đường tròn (O) tại C. Tứ giác OCBM là hình gì? Vì sao?
( Thị phạm cho cái hình vẽ nhé 🎨 thanh kiu, mong cao nhân biết giải hộ nhanh chiều tại hạ đi thi lại)
Quảng cáo
2 câu trả lời 3451
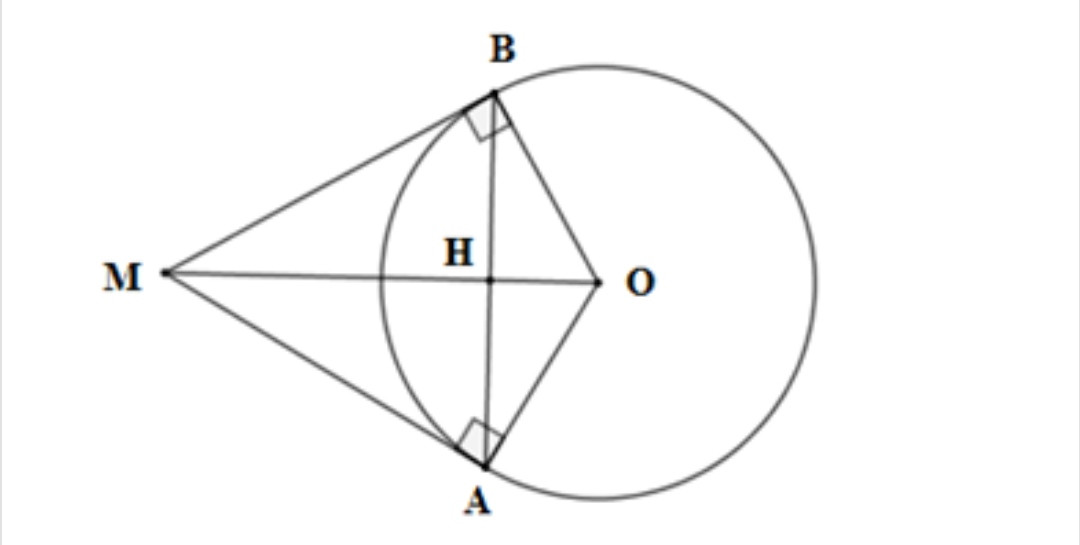
a) xét đường tròn (O) MA=MB (Tính chất 2 tiếp tuyến cắt nhau)
Xét tam giác MAB cân tại M, =60°
=> MAB=MBA=(180 độ -góc AMB)/2=60
=> Tam giác AMB là tam giác đều (tổng 3 góc =60)
b) Ta có: OA=OB(=R) và MA=MB
=> OM là đường trung trực của AB
=> OM vuông góc AB
Mà tam giác AMB cân tại M nên đường cao OM đồng thời cũng là đường phân giác
=> Góc AMO=(góc AMB)/2=30
MA vuông góc OA(MA là tiếp tuyến của (o))
Xét tam giác MAO vuông tại A, có: tan(AMO)=AO/AM<=>√3/3=5/AM
=> AM=5√3
c) Lấy I là giao điểm của AB và MO
Ta có góc BIO=90
Mặt khác AO∩(O)=C=> AC là đường kính của (O)
=> góc ABC=90
=> MO//BC
=> Tứ giác BMOC là hình thang
a) Theo tính chất của hai đường tiếp tuyến cắt nhau thì MA=MBMA=MB
Xét tam giác MABMAB cân tại MM có ∠AMB=600∠AMB=600 nên :
∠MAB=∠MBA=1800−∠AMB2=600∠MAB=∠MBA=1800−∠AMB2=600
Tam giác có cả ba góc đều bằng 600600 nên là tam giác đều.
b) {OA=OBMA=MB⇒MO{OA=OBMA=MB⇒MO là trung trực của ABAB, do đo MO⊥ABMO⊥AB
Mà tam giác MABMAB cân tại MM nên đường cao MOMO đồng thời cũng là đường phân giác. Do đó ∠AMO=∠AMB2=300∠AMO=∠AMB2=300
Vì MAMA là tiếp tuyến của (O)(O) nên MA⊥OAMA⊥OA
Xét tam giác MAOMAO vuông tại AA có:
tan∠AMO=AOAM⇔√33=5AMtan∠AMO=AOAM⇔33=5AM ⇒AM=5√3⇒AM=53
Vì AMBAMB là tam giác đều nên chu vichu vi (AMB) là:
P=3AM=15√3P=3AM=153
c) Lấy II là giao điểm của ABAB và MOMO. Ta có ∠BIO=900∠BIO=900
Mặt khác AO∩(O)=C⇒ACAO∩(O)=C⇒AC là đường kính của (O)(O)
⇒∠ABC=900⇒∠ABC=900
Từ hai điều trên suy ra MO∥BCMO∥BC . Như vật BMOCBMOC là hình thang
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490


