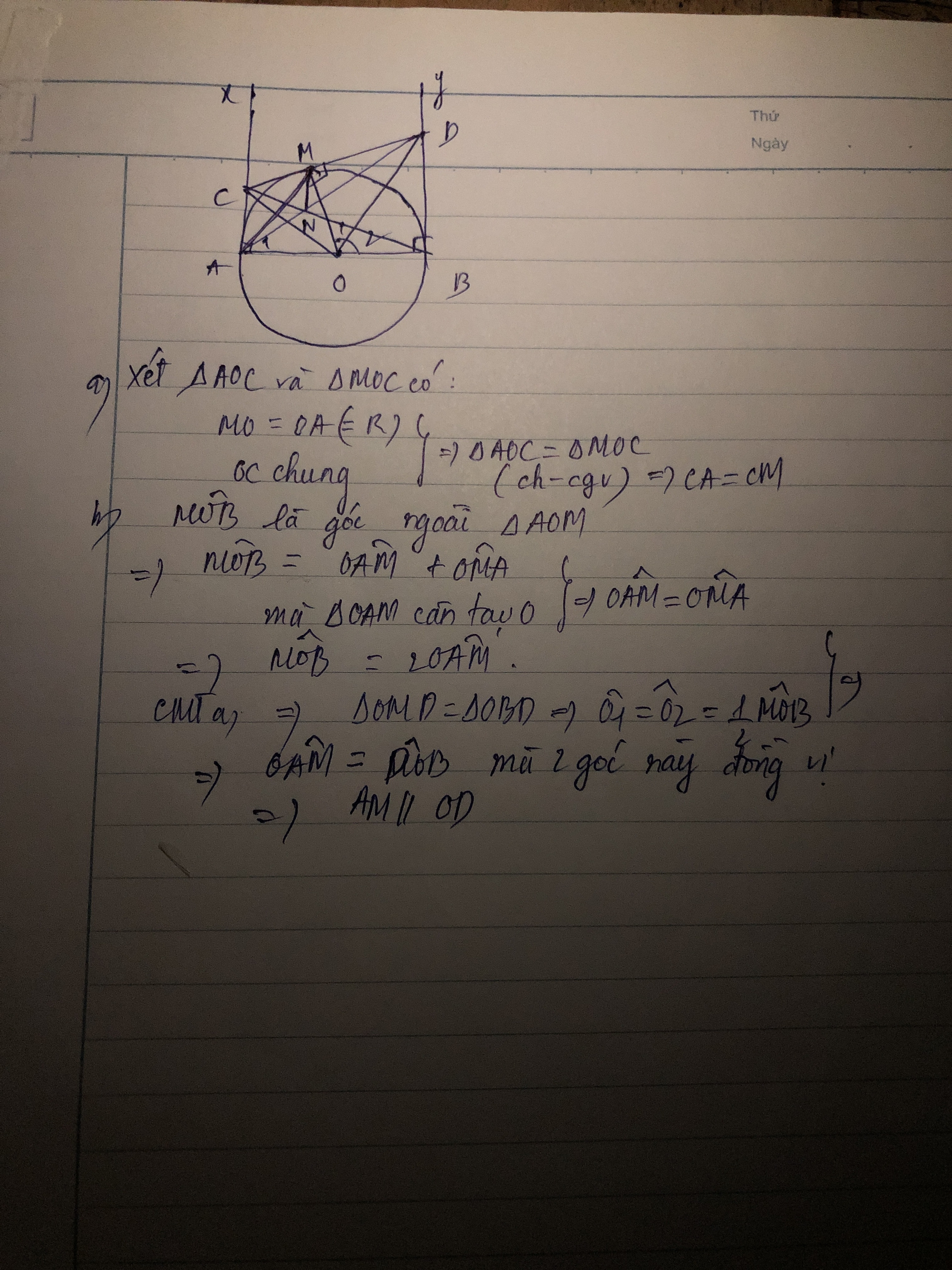Cho nửa dường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc nửa đường tròn (M khác A và B). Đường thăng qua M vuông góc với OM cắt Ax tại C và cắt By tại D. a) Chứng minh CA=CM. b) Chứng minh MOB = 2. MAO, từ đó suy ra AM song song với OD. c) Gọi N là giao điểm của AD và BC. Chứng minh đường thẳng MN vuông góc với đường thẳng AB.
Quảng cáo
2 câu trả lời 1522
3 năm trước
Cho nửa dường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc nửa đường tròn (M khác A và B). Đường thăng qua M vuông góc với OM cắt Ax tại C và cắt By tại D. a) Chứng minh CA=CM. b) Chứng minh MOB = 2. MAO, từ đó suy ra AM song song với OD. c) Gọi N là giao điểm của AD và BC. Chứng minh đường thẳng MN vuông góc với đường thẳng AB.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274
Gửi báo cáo thành công!