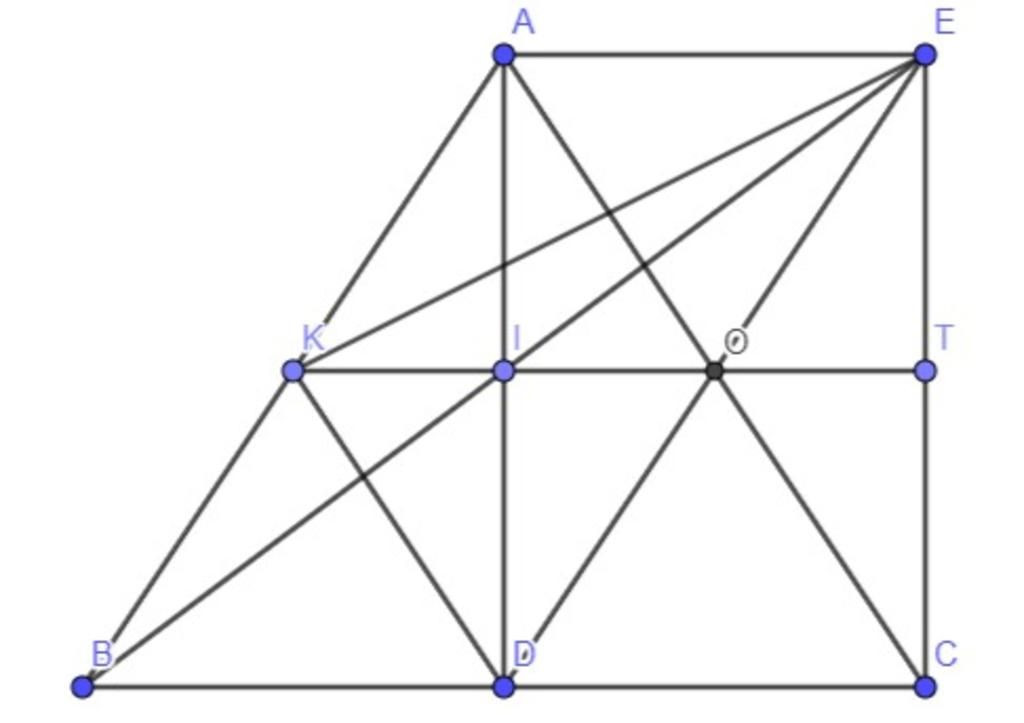
Bài `4.`
`a)`
`E` đối xứng với `D` qua `O`
`=>O` là trung điểm của `DE`
Xét tứ giác `ADCE` có:
Hai đường chéo `DE` và `AC` cắt nhau tại trung điểm `O` của mỗi đường
`=>` Tứ giác `ADCE` là hình bình hành
Mà `hat{ADC}=90^o(ADbotDC)`
`=>` Hình bình hành `ADCE` là hình chữ nhật
`b)`
Xét `ΔADC` có:
`I` là trung điểm của `AD`
`O` là trung điểm của `AC`
`=>IO` là đường trung bình của `ΔADC`
`=>\text{IO}////BD`
Trong `ΔBDE` có:
`O` là trung điểm của `DE`
`\text{IO}////BD`
`=>I` là trung điểm của `BE`
`c)`
`ΔABC` cân có `AD` đường cao
`=>AD` đồng thời là đường trung tuyến
`=>D` là trung điểm của `BC`
`=>BD=(BC)/2=12/2=6(cm)`
`ΔABD` vuông tại `D` nên theo pi-ta-go
`AB^2=BD^2+AD^2`
`=>AD=sqrt{AB^2-BD^2}=sqrt{10^2-6^2}=8(cm)`
Gọi `T` là trung điểm của `EC` 
Trong `ΔBEC` có:
`T` là trung điểm của `EC`
`I` là trung điểm của `BE`
`=>IT` là đường trung bình của `ΔBEC`
`=>IT////BD` mà `\text{IO}////BD`
`=>I;O;T` thẳng hàng
Từ `IT////BD` hay `IT////DC`
Xét tứ giác `IDCT` có:
`ID////TC(cmt);IT////CD(cmt)`
`=>` Tứ giác `IDCT` là hình bình hành 
`=>IT=DC=6cm(DC=(BC)/2=6cm)`
`AEDC` là hình chữ nhật
`=>AC=DE`
`=>(AC)/2=(DE)/2`
`=>OD=OC`
`IDCT` là hình bình hành có `hat{IDC}=90^o`
`=>IDCT` là hình chữ nhật
Xét `ΔIOD` và `ΔTOC` có:
`ID=TC(IDCT` là hình chữ nhật)
`OA=OC(cmt)`
`hat{OID}=hat{OTC}=90^o`
`=>ΔIOD=ΔTOC(text{cạnh huyền-cạnh góc vuông})`
`=>IO=TO`
`=>O` là trung điểm của `IT`
`=>OI=(IT)/2=6/2=3(cm)`
`=>S_(ΔADO)=1/2 . AD . OI=1/2 . 8 . 3=12(cm^2)`
`d)`
`AE////DC` hay `AE////BD`
`AE=DC(ADCE` là hình chữ nhật)
Mà `BD=DC(D` là trung điểm của `BC`)
`=>AE=BD`
Xét tứ giác `AEDB` có:
`AE////DB(cmt);AE=BD(cmt)`
`=>` Tứ giác `AEDB` là hình bình hành 
`=>AK////DE`
`=>` Tứ giác `AKDE` là hình thang 
Giả sử `ΔABC` là tam giác đều
`\text{IO}////BD` hay `IK////BD`
Trong `ΔABD` có:
`I` là trung điểm của `AD`
`IK////BD`
`=>K` là trung điểm của `AB`
Trong tam giác `ABC` có `KD` là đường trung bình
`=>KD=1/2AC=1/2AB=1/2BC`
`=>KD=KB=BD`
`=>ΔKBD` đều
Trong `ΔABC` có `OD` là đường trung bình
`=>OD=1/2AB=1/2BC=1/2AC`
`=>OD=DC=OC`
`=>ΔODC` đều
`=>hat{KDE}=180^o - 60^o - 60^o=60^o`
`ΔDCE` vuông tại `C`
`=>hat{DEC}=180^o - 90^o - 60^o=30^o`
Lại có:
`hat{DEC}+hat{AED}=90^o`
`=>hat{AED}=90^o - 30^o=60^o`
`=>hat{AED}=hat{KDE}=60^o`
`=>` hình thang `AKDE` là hình thang cân
Vậy tam giác `ABC` đều thì tứ giác `AKDE` là hình thang cân
Bài `5.`
`P=(2bc-2016)/(3c-2bc+2016)-(2b)/(3-2b+ab)+(4032-3ac)/(3ac-4032+2016a)`
`P=(2bc-abc)/(3c-2bc+abc)-(2b)/(3-2b+ab)+(2abc-3ac)/(3ac-2abc+abc.a)`
`P=(2bc-abc)/(3c-2bc+abc)-(2bc)/(3c-2bc+abc)+(2bc-3c)/(3c-2bc+abc)`
`P=(2bc-abc-2bc+2bc-3c)/(3c-2bc+abc)`
`P=(2bc-abc-3c)/(3c-2bc+abc)`
`P=(-(3c-2bc+abc))/(3c-2bc+abc)`
`P=-1`
Vậy `P=-1`