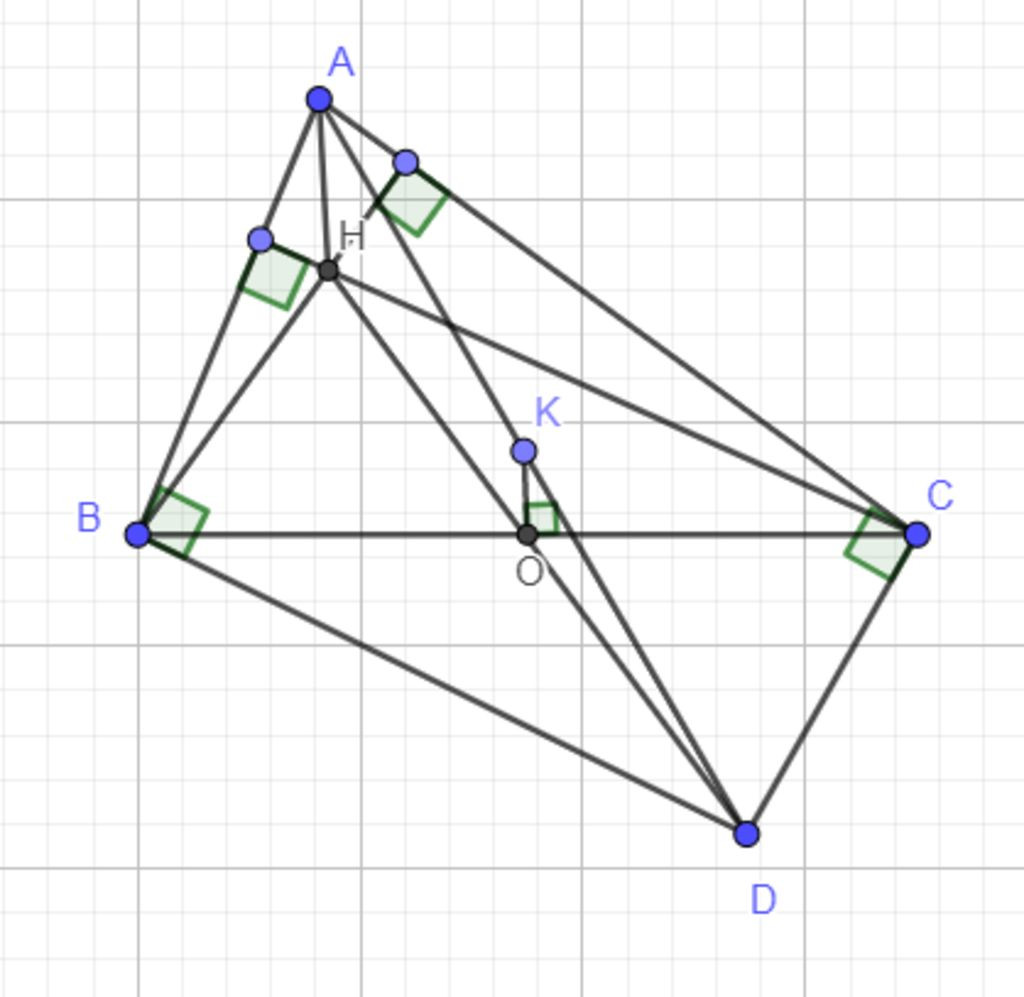
Cho tam giác ABC có trực tâm H, kẽ Bx vuông góc với AB, Cy vuông góc với AC. Gọi D là giao điểm của Bx và Cy. a) Chứng minh: Tứ giác BHCD là hình bình hành. b) Gọi O là trung điểm của BC. Chứng minh: 3 điểm H, O, D thẳng hàng. c) Đường thẳng vuông góc với BC tại O cắt AD tại K. Chứng minh: AH=2.OK
Quảng cáo
2 câu trả lời 5023
`a.`
Ta có: `Bx////CH` (cùng vuông góc `AB`)
`Cy////BH` (cùng vuông góc `AC`)
`=>BD////CH, CD////BH`
nên tứ giác `BHCD` là hình bình hành.
`b.`
Do `O` là trung điểm `BC`
mà tứ giác `BHCD` là hình bình hành
`=>` Đường chéo `HD` phải đi qua `O`
`=>H,O,D` thẳng hàng.
`c.`
`H` là trực tâm nên `AH⊥BC`
mà `OK⊥BC`
`=>OK////AH`
Xét `DeltaDHA` có: `OK////AH`
`=>(DO)/(DH)=(DK)/(DA)=(OK)/(AH)`
mà `O` là trung điểm `HD`
`=>K` là trung điểm `AD`
nên `OK` là đường trung bình `DeltaDHA`
`=>OK=2AH`
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274

 Tham khảo !!
Tham khảo !!
