$\color{darkgoldenrod}{a)}$   Xét $(O)$ có:

$\hspace{0.65cm}\ AB$ là tiếp tuyến $\Rightarrow\ AB\bot BO\ \Rightarrow\ \widehat{ABO}=90^\circ\ \Rightarrow\ B\in$ đường tròn đường kính $OA\ \ \ \ \ (1)$

$\hspace{0.65cm}\ AC$ là tiếp tuyến $\Rightarrow\ AC\bot CO\ \Rightarrow\ \widehat{ACO}=90^\circ\ \Rightarrow\ C\in$ đường tròn đường kính $OA\ \ \ \ \ (2)$

$\hspace{0.65cm}$ Từ $(1),(2)\ \Rightarrow\ A,B,O,C$ cùng thuộc 1 đường tròn $(đpcm)$

$\\$

$\color{darkgoldenrod}{b)}$   Xét $\triangle ABO$ vuông tại $B$ có:

$\hspace{0.65cm}\ OB^2+AB^2=OA^2\ \ \ (đ/l Pitago)$

$\hspace{0.65cm}$ Mà $OB=R;\ OA=2R\ \ (gt)$

$\Rightarrow\ R^2+AB^2=(2R)^2$

$\Leftrightarrow\ AB^2=4R^2-R^2$

$\Leftrightarrow\ AB^2=3R^2$

$\Leftrightarrow\ AB=R\sqrt{3}$

$\hspace{0.65cm}$ Xét $(O)$ có:

$\hspace{0.65cm}\ \widehat{ABM}$ là góc tạo bởi tiếp tuyến và dây cung chắn cung $BM$

$\hspace{0.65cm}\ \widehat{BNM}$ là góc nội tiếp chắn cung $BM$

$\Rightarrow\ \widehat{ABM}=\widehat{BNM}$ (t/c đường tròn)

$\hspace{0.65cm}$ Xét $\triangle ABM$ và $\triangle ANB$ có:

$\hspace{0.65cm}\ \widehat{BAN}$ chung

$\hspace{0.65cm}\ \widehat{ABM}=\widehat{BNM}\ \ (cmt)$

$\Rightarrow\ \triangle ABM\ \backsim\ \triangle ANB\ \ (g-g)$

$\Rightarrow\ \dfrac{AB}{AN}=\dfrac{AM}{AB}$ (t/c $\triangle$ đồng dạng)

$\Leftrightarrow\ AM.\ AN=AB^2$

$\Leftrightarrow\ AM.\ AN=3R^2\ \ (cmt)\ (đpcm)$

$\\$

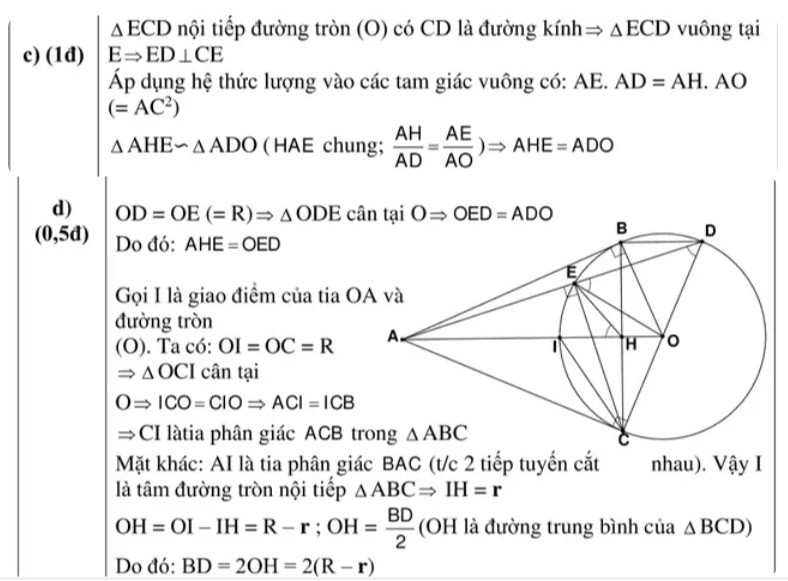
$\color{darkgoldenrod}{c)}$   Ta có:

$\hspace{0.65cm}\ S_{phần\ nằm\ ngoài\ (O)}=S_{ABOC}-S_{hình\ quạt\ OBC}$

$\hspace{0.65cm}$ Xét $\triangle \bot ABO$ và $\triangle \bot ACO$ có: 

$\hspace{0.65cm}\ OB=OC=R$

$\hspace{0.65cm}\ OA$ chung

$\Rightarrow\ \triangle \bot ABO=\triangle \bot ACO\ \ (ch-cgv)$

$\Rightarrow\ S_{ABOC}=S_{\triangle \bot ABO}+S_{\triangle \bot ACO}$

$\hspace{0.65cm}\ =2S_{\triangle \bot ABO}$

$\hspace{0.65cm}\ =\dfrac{AB.\ OB}{2}$

$\hspace{0.65cm}\ =\dfrac{R\sqrt{3}.\ R}{2}$

$\hspace{0.65cm}\ =\dfrac{R^2\sqrt{3}}{2}$ 

$\hspace{0.65cm}$ Xét $\triangle ABO$ vuông tại $B$ có:

$\hspace{0.65cm}\ cos\widehat{BOA}=\dfrac{OB}{OA}=\dfrac{R}{2R}=\dfrac{1}{2}$

$\Rightarrow\ \widehat{BOA}=60^\circ$

$\Rightarrow\ \triangle \bot ABO=\triangle \bot ACO\ \ (cmt)$

$\Rightarrow\ \widehat{BOA}=\widehat{COA}$

$\Rightarrow\ \widehat{BOC}=\widehat{BOA}+\widehat{COA}=2\widehat{BOA}=120^\circ$

$\Rightarrow\ S_{hình\ quạt\ OBC}=\dfrac{R^2.\ 120^\circ}{360^\circ}=\dfrac{R^2}{3}$

$\Rightarrow\ S_{phần\ nằm\ ngoài\ (O)}=S_{ABOC}-S_{hình\ quạt\ OBC}$

$\hspace{0.65cm}\ =\dfrac{R^2\sqrt{3}}{2}-\dfrac{R^2}{3}$

$\hspace{0.65cm}\ =\dfrac{3R^2\sqrt{3}-2R^2}{6}$

$\hspace{0.65cm}\ =\dfrac{3\sqrt{3}-2}{6}R^2$