Cho tam giác ABC và ABD cùng vuông tại A như Hình 3 có AB = x, BC = 5 và BD = 6
Lời giải Bài 10 trang 23 SBT Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Bài 10 trang 23 SBT Toán 10 Tập 2: Cho tam giác ABC và ABD cùng vuông tại A như Hình 3 có AB = x, BC = 5 và BD = 6.
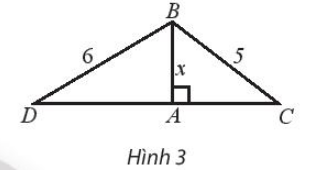
a) Biểu diễn độ dài cạnh AC và AD theo x.
b) Tìm x để chu vi của tam giác ABC là 12.
c) Tìm x để AD = 2AC
Lời giải:
a) Vì x là khoảng cách AB nên x > 0
Áp dụng định lí Phytagoras cho tam giác ABC:
AB2 + AC2 = BC2
⇒ AC2 = 52 – x2
Như vậy AC =
Áp dụng định lí Phytagoras cho tam giác ABD:
AB2 + AD2 = BD2
⇒ AD2 = 62 – x2
Như vậy AD =
b) Giải phương trình AB + AC + BC = 12
⇒ x + 5 + = 12
⇒ = 7 – x
⇒ 25 – x2 = (7 – x)2
⇒ 2x2 – 14x + 24 = 0
⇒ x = 4 hoặc x = 3
Thay lần lượt các giá trị trên vào phương trình AB + AC + BC = 12 ta thấy x = 4 và x = 3 đều thoả mãn. Vậy x = 4 hoặc x = 3 để chu vi tam giác ABC là 12.
c) Ta có AD = 2AC
⇒ = 2
⇒ 36 – x2 = 100 – 4x2
⇒ 3x2 – 64 = 0
⇒ x = hoặc x = mà x > 0 nên x = .
Thay x = vào phương trình AD = 2AC thấy thỏa mãn. Vậy x = .
Xem thêm các bài giải sách bài tập Toán 10 bộ sách Chân trời sáng tạo hay, chi tiết khác:
Câu 1 trang 19 SBT Toán 10 Tập 2: Tam thức bậc hai nào có biệt thức ∆ = 1 và hai nghiệm là: và ...
Câu 2 trang 19 SBT Toán 10 Tập 2: Tam thức bậc hai nào dương với mọi ?...
Câu 3 trang 19 SBT Toán 10 Tập 2: Khẳng định nào sau đây đúng với tam thức bậc hai ...
Câu 5 trang 20 SBT Toán 10 Tập 2: Cho đồ thị của hàm số bậc hai y = f(x) như Hình 1 Tập nghiệm của bất phương trình là...
Câu 6 trang 20 SBT Toán 10 Tập 2: Bất phương trình nào có tập nghiệm là (2; 5)?...
Câu 7 trang 20 SBT Toán 10 Tập 2: Tập xác định của hàm số là...
Câu 9 trang 20 SBT Toán 10 Tập 2: Giá trị nào là nghiệm của phương trình
Câu 10 trang 20 SBT Toán 10 Tập 2: Khẳng định nào đúng với phương trình
Câu 11 trang 20 SBT Toán 10 Tập 2: Khẳng định nào đúng với phương trình
Bài 2 trang 21 SBT Toán 10 Tập 2: Xét dấu của các tam thức bậc hai sau...
Bài 3 trang 21 SBT Toán 10 Tập 2: Giải các bất phương trình bậc hai sau...
Bài 5 trang 22 SBT Toán 10 Tập 2: Giải các phương trình sau...
Bài 6 trang 22 SBT Toán 10 Tập 2: Tìm tập xác định của các hàm số sau...
Bài 7 trang 22 SBT Toán 10 Tập 2: Tìm các giá trị của tham số m để: a) là một tam thức bậc hai âm với mọi ...
Bài viết liên quan
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài 1: Dấu của tam thức bậc hai
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài 2: Giải bất phương trình bậc hai một ẩn
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài 3: Phương trình quy về phương trình bậc hai
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài tập cuối chương 7
