Bài 3 trang 21 SBT Toán 10 Tập 2: Giải các bất phương trình bậc hai sau:

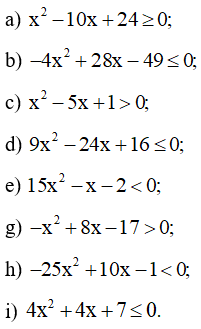
Lời giải:

a) $x^2-10x+24\ge 0;$

Tam thức bậc hai f ( x ) = x² – 10x + 24 có ∆ = (– 10)² – 4.1.24 = 4 > 0 suy ra f(x) có hai nghiệm phân biệt x₁ = 6 và x₂ = 4 và a = 1 > 0 nên f ( x ) > 0 với x ≤ 4 hoặc x ≥ 6.

Vậy bất phương trình đã cho có tập nghiệm S = (– ∞; 4] ∪ [6; +∞)

b) $-4x^2+28x-49\le 0;$

Tam thức bậc hai f ( x ) = –4x² + 28x – 49 có ∆ = 28² – 4.(– 4).(– 49) = 0 suy ra f(x) có một nghiệm x = $\frac{7}{2}$ , a = –4 < 0 nên f ( x ) ≤  0 với mọi x ∈ ℝ.

Vậy bất phương trình đã cho có tập nghiệm S = ℝ.

c) $x^2-5x+1>0;$

Tam thức bậc hai f ( x ) = x² – 5x + 1 có ∆ = (–5)² – 4.1.1 = 21 suy ra f(x) có hai nghiệm phân biệt x₁ = $\frac{5+\sqrt{21}}{2}$ và x₂ = $\frac{5-\sqrt{21}}{2}$, a = 1 > 0 nên f ( x ) > 0 với x < $\frac{5-\sqrt{21}}{2}$ hoặc x > $\frac{5+\sqrt{21}}{2}$.

Vậy bất phương trình đã cho có tập nghiệm S = $\left(-\infty ;\frac{5-\sqrt{21}}{2}\right)\cup \left(\frac{5+\sqrt{21}}{2};+\infty \right)$

d) $9x^2-24x+16\le 0;$

Tam thức bậc hai f ( x ) = 9x² – 24x +16 có ∆ = (–24)² – 4.9.16 = 0 suy ra f(x) có một nghiệm x = $\frac{4}{3}$ , a = 9 > 0 nên f ( x ) ≤  0 khi x = $\frac{4}{3}$.

Vậy bất phương trình đã cho có tập nghiệm S = $\left\{\frac{4}{3}\right\}$

e) $15x^2-x-2<0;$

Tam thức bậc hai f ( x ) = 15x² – x – 2 có ∆ = (–1)² – 4.15.( –2) = 121 suy ra f(x) có hai nghiệm phân biệt x₁ = $\frac{2}{5}$ và x₂ = $\frac{-1}{3}$, a = 15 > 0 nên f ( x ) < 0 với $\frac{-1}{3}$ < x < $\frac{2}{5}$.

Vậy bất phương trình đã cho có tập nghiệm S = $\left(\frac{-1}{3};\frac{2}{5}\right)$

g) $-x^2+8x-17>0;$

Tam thức bậc hai f ( x ) = –x² + 8x – 17 có ∆ = 8² – 4.( –1).( –17) = –4 < 0 , a = –1 < 0 nên f ( x ) âm với mọi x ∈ ℝ.

Vậy bất phương trình vô nghiệm.

h) $-25x^2+10x-1<0;$

Tam thức bậc hai f ( x ) = –25x² + 10x – 1 có ∆ = 10² – 4.( –25).( –1) = 0  suy ra f(x) có một nghiệm x = $\frac{1}{5}$ , a = –25 < 0 nên f ( x ) < 0 khi x ≠ $\frac{1}{5}$.

Vậy bất phương trình đã cho có tập nghiệm S = ℝ \ $\frac{1}{5}$.

i) $4x^2+4x+7\le 0.$

Tam thức bậc hai f ( x ) = 4x² + 4x + 7 có ∆ = 4² – 4.4.7 = –96 < 0 , a = 4 > 0 nên f ( x ) dương với mọi x ∈ ℝ.

Vậy bất phương trình vô nghiệm.