Cho ba điểm A(- 2; 2), B(4; 2), C(6; 4). Viết phương trình đường thẳng ∆ đi qua B
Lời giải Bài 45 trang 82 SBT Toán 10 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Bài 45 trang 82 SBT Toán 10 Tập 2: Cho ba điểm A(- 2; 2), B(4; 2), C(6; 4). Viết phương trình đường thẳng ∆ đi qua B đồng thời cách đều A và C?
Lời giải:
cách đều A và C khi và chỉ khi đi qua trung điểm của AC hoặc song song với AC.
TH1: ∆ là đi qua trung điểm của AC
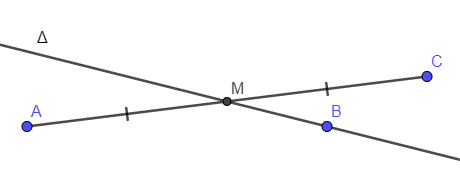
Gọi M là trung điểm của đoạn thẳng AB nên tọa độ điểm M là M(2; 3).
Vectơ chỉ phương của đường thẳng ∆ là:
Suy ra vectơ pháp tuyến của đường thẳng ∆ là:
Do đó phương trình đường thẳng là: x – 2 + 2(y – 3) = 0 ⇔ x + 2y – 8 = 0
TH2: ∆ song song với AC.
Vectơ chỉ phương của đường thẳng ∆ là: nên vectơ pháp tuyến của đường thẳng ∆ là:
Phương trình đường thẳng ∆ là: x – 4 – 4(y – 2) = 0 ⇔ x – 4y + 4 = 0.
Xem thêm các bài giải sách bài tập Toán 10 bộ sách Cánh diều hay, chi tiết khác:
Bài 38 trang 82 SBT Toán 10 Tập 2: Cho và . Số đo góc giữa hai đường thẳng ∆1 và ∆2 là...
Bài 40 trang 82 SBT Toán 10 Tập 2: Xét vị trí tương đối của mỗi cặp đường thẳng sau: a) d1: 2x – 3y + 5 = 0 và d2: 2x + y – 1 = 0...
Bài 41 trang 82 SBT Toán 10 Tập 2: Tìm số đo góc giữa hai đường thẳng của mỗi cặp đường thẳng sau: a) ∆1: 3x + y – 5 = 0 và ∆2: x + 2y – 3 = 0...
Bài 42 trang 82 SBT Toán 10 Tập 2: Tính khoảng cách từ một điểm đến một đường thẳng trong các trường hợp sau: a) A(- 3; 1) và ∆1: 2x + y – 4 = 0...
Bài 44 trang 82 SBT Toán 10 Tập 2: Cho hai đường thẳng ∆1: mx – 2y – 1 = 0 và ∆2: x – 2y + 3 = 0. Với giá trị nào của tham số m thì: a) ∆1 // ∆2...
Bài viết liên quan
- Giải Sách bài tập Toán 10 Cánh diều Bài 3: Phương trình đường thẳng
- Giải Sách bài tập Toán 10 Cánh diều Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
- Giải Sách bài tập Toán 10 Cánh diều Bài 5: Phương trình đường tròn
- Giải Sách bài tập Toán 10 Cánh diều Bài 6: Ba đường conic
- Giải Sách bài tập Toán 10 Cánh diều Bài tập cuối chương 7
