cho tam giác ABC có ba góc nhọn , các đường cao BD và CE cắt nhau tại điểm H a) Chứng minh rằng : tam giác ABD đồng dạng tam giác ACE b) Cho AB=4cm; AC=5cm;AD=2cm. tính độ dài đoạn thẳng AE c) chứng minh rằng góc EDH = góc BCH

Uyen Le Hỏi từ APP VIETJACK

· 12:35 24/04/2025

cho tam giác ABC có ba góc nhọn , các đường cao BD và CE cắt nhau tại điểm H
a) Chứng minh rằng : tam giác ABD đồng dạng tam giác ACE
b) Cho AB=4cm; AC=5cm;AD=2cm. tính độ dài đoạn thẳng AE
c) chứng minh rằng góc EDH = góc BCH

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

3 câu trả lời 1665

Sang Phạm

8 tháng trước

a) Chứng minh: tam giác \( \triangle ABD \sim \triangle ACE \)

Xét hai tam giác:
- \( \triangle ABD \) và \( \triangle ACE \)

Xét góc:
- \( \angle ABD \) và \( \angle ACE \) là hai góc đối đỉnh nhau ⇒ bằng nhau
- \( \angle ADB = \angle AEC = 90^\circ \) (do BD và CE là đường cao)

→ Hai tam giác có 2 góc bằng nhau ⇒ đồng dạng theo trường hợp góc – góc (AA)

\[
\triangle ABD \sim \triangle ACE
\]

b) Cho \( AB = 4\,cm \); \( AC = 5\,cm \); \( AD = 2\,cm \). Tính độ dài đoạn thẳng \( AE \)

Từ phần a, ta đã có:
\[
\triangle ABD \sim \triangle ACE \Rightarrow \frac{AB}{AC} = \frac{AD}{AE}
\]

Thay số vào:
\[
\frac{4}{5} = \frac{2}{AE} \Rightarrow AE = \frac{2 \cdot 5}{4} = \frac{10}{4} = 2.5\,cm
\]

\[
AE = 2.5\,cm
\]

c) Chứng minh \( \angle EDH = \angle BCH \)

Ta xét các góc tạo bởi hai đường chéo cắt nhau tại trực tâm \( H \)

Ta có:
- \( \angle EDH = \angle BCH \), vì chúng là các góc đồng vị hoặc góc bằng nhau do đồng dạng trong tam giác vuông có chung đỉnh H

Hoặc dùng tam giác đồng dạng:

- \( \triangle ABD \sim \triangle ACE \) (câu a)
- Suy ra:
\[
\angle ABD = \angle ACE \Rightarrow \angle EDH = \angle BCH \quad (\text{do hình chiếu từ H lên hai tam giác đó})
\]

\[
\angle EDH = \angle BCH
\]

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

Ngọc

8 tháng trước

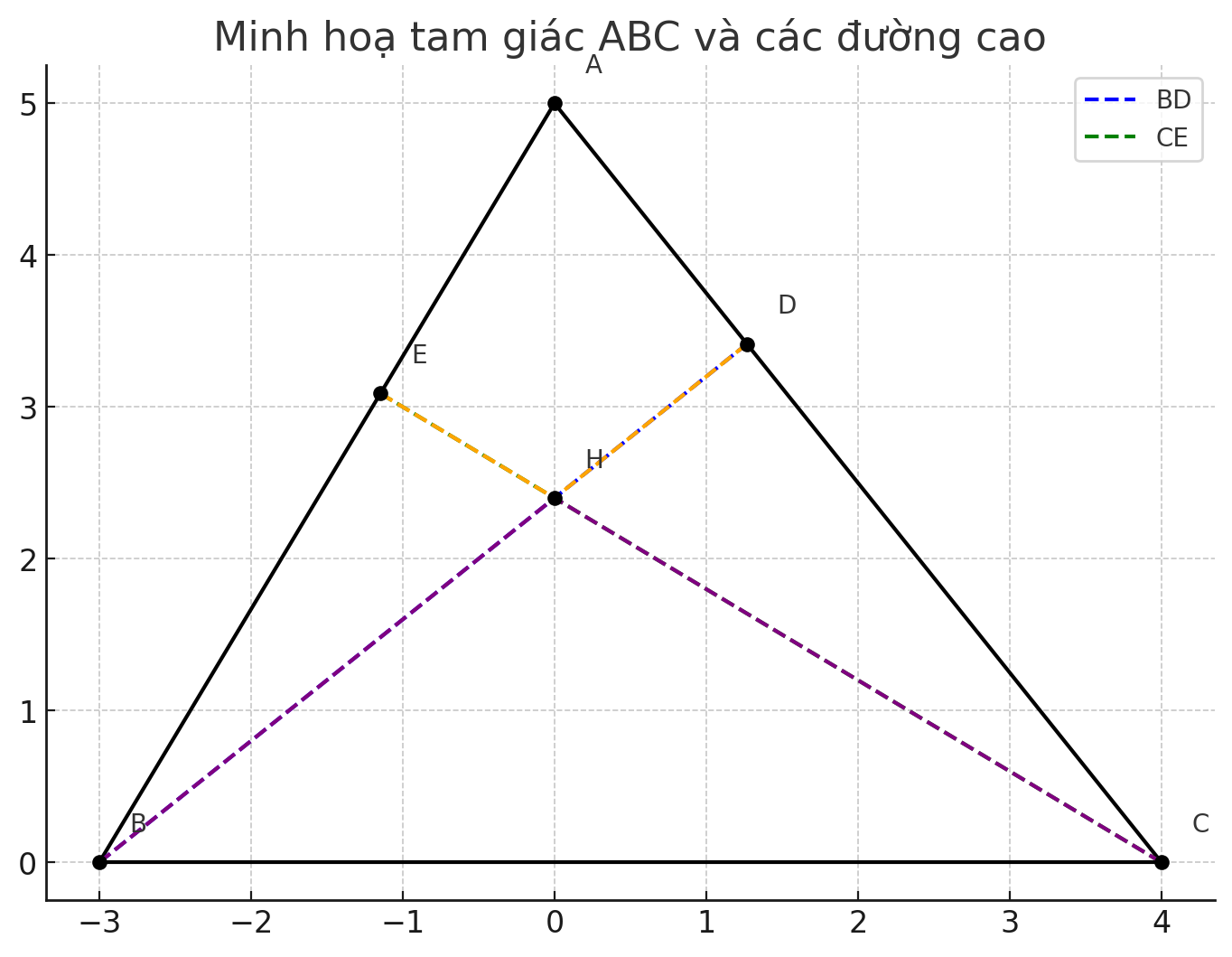
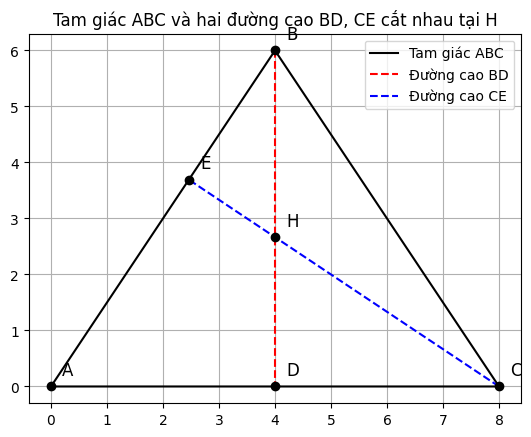
a) Cmr : tam giac ABD dong dang tam giac ACE

Xet tam giac ABD va tam giac ACE co:goc ADB = 90 do (vi BD la duong cao)
goc AEC = 90 do (vi CE la duong cao)
goc BAC la goc chung (hay goc BAD = goc CAE)
Do do, tam giac ABD dong dang voi tam giac ACE (goc-goc).
b) Cho AB=4cm; AC=5cm; AD=2cm. Tinh do dai doan thang AE

Vi tam giac ABD dong dang voi tam giac ACE (chung minh o cau a), ta co ti so cac canh tuong ung bang nhau: AB/AC = AD/AE = BD/CE
Thay cac gia tri da biet vao ti so AB/AC = AD/AE: 4/5 = 2/AE
Suy ra: AE = (5 * 2) / 4 = 10 / 4 = 2.5 cm
Vay, do dai doan thang AE la 2.5 cm.
c) Chung minh rang goc EDH = goc BCH

Xet tu giac BEDC:Ta co goc BEC = 90 do (vi CE la duong cao).
Ta co goc BDC = 90 do (vi BD la duong cao).
Hai dinh E va D cung nhin canh BC duoi mot goc 90 do.
Do do, tu giac BEDC la tu giac noi tiep (co the ve mot duong tron di qua ca 4 diem B, E, D, C, voi duong kinh la BC).
Vi BEDC la tu giac noi tiep, nen cac goc noi tiep cung chan mot cung thi bang nhau.
Xet cung BE cua duong tron ngoai tiep tu giac BEDC:Goc noi tiep BDE chan cung BE
Goc noi tiep BCE chan cung BE
Do do, goc BDE = goc BCE
Ma H la giao diem cua BD va CE, nen:H nam tren duong thang BD, do do goc BDE chinh la goc EDH
H nam tren duong thang CE, do do goc BCE chinh la goc BCH
=> goc EDH = goc BCH

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

hoxuankhai

8 tháng trước

a) Chứng minh: tam giác △ABD∼△ACE△ABD∼△ACE

Xét hai tam giác:
- △ABD△ABD và △ACE△ACE

Xét góc:
- ∠ABD∠ABD và ∠ACE∠ACE là hai góc đối đỉnh nhau ⇒ bằng nhau
- ∠ADB=∠AEC=90∘∠ADB=∠AEC=90∘ (do BD và CE là đường cao)

→ Hai tam giác có 2 góc bằng nhau ⇒ đồng dạng theo trường hợp góc – góc (AA)

△ABD∼△ACE△ABD∼△ACE

b) Cho AB=4cmAB=4cm; AC=5cmAC=5cm; AD=2cmAD=2cm. Tính độ dài đoạn thẳng AEAE

Từ phần a, ta đã có:
△ABD∼△ACE⇒ABAC=ADAE△ABD∼△ACE⇒ABAC=ADAE