a) Chứng minh tam giác ABE = tam giác DBE

Xét hai tam giác ABE và DBE:

- Có:
+ $BA = BD$ (giả thiết)
+ $BE$ chung
+ $\angle ABE = \angle DBE$ (cùng là góc kề bù tạo bởi đường thẳng cắt nhau tại điểm B)

⇒ ΔABE = ΔDBE (c.g.c)

b) Gọi F là giao điểm của DE và BA, chứng minh EF = EC

Từ tam giác ABE = tam giác DBE (câu a):
⇒ $AE = DE$

Xét tam giác DEC, có:
- DE ⊥ BC (giả thiết)
- Gọi F là giao điểm của DE và BA
- Tam giác DEC có đường cao DE, cắt AC tại E
- Vì AE = DE (từ câu a), nên E là trung điểm của đoạn AC và DF

⇒ Tam giác DEF cân tại E → $EF = EC$

(Ta có thể suy ra điều này do tam giác cân tại E, hoặc từ tam giác vuông cân khi E là trung điểm của đoạn thẳng và D đối xứng với A qua trung điểm đó)

c) Chứng minh AD // FC

- Từ b) ta đã có $EF = EC$
- Xét tam giác DEC với E là điểm chung:
+ D thuộc BC, F thuộc BA
+ C thuộc AC

→ Tứ giác ADFC là hình thang vì AD và FC cùng vuông góc với DE

⇒ AD // FC

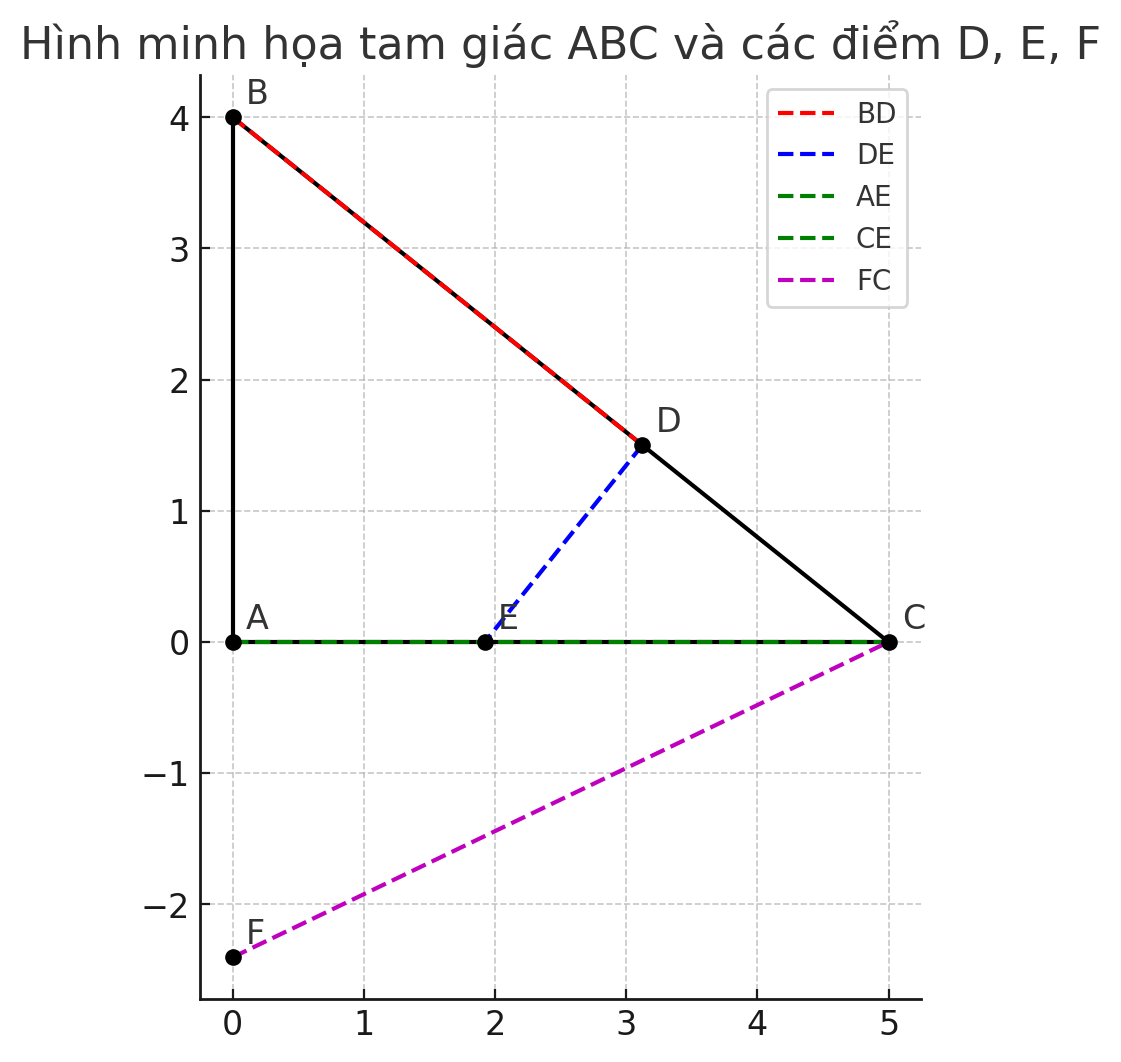
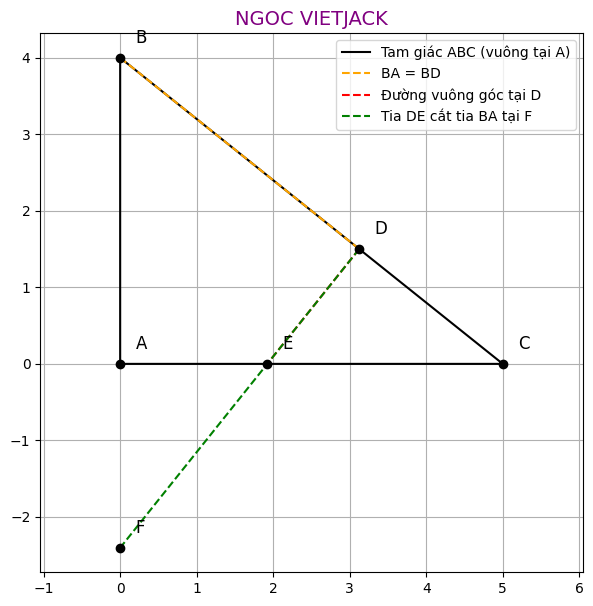
a) Chứng minh tam giác ABE = tam giác DBE:

Xét tam giác ABE và tam giác DBE, ta có:Góc BAE = 90 độ (vì tam giác ABC vuông tại A)
Góc BDE = 90 độ (vì DE vuông góc BC tại D)
Cạnh BE là cạnh chung.
BA = BD (theo giả thiết).
Do đó, tam giác ABE = tam giác DBE (theo trường hợp bằng nhau cạnh huyền - cạnh góc vuông).
b) Gọi F là giao điểm của DE và BA, chứng minh EF = EC:

Xét tam giác AFE và tam giác DCE, ta có:Góc FAE = Góc CDE = 90 độ.
AE = DE (vì tam giác ABE = tam giác DBE theo chứng minh ở câu a, đây là hai cạnh tương ứng).
Góc AEF = Góc DEC (hai góc đối đỉnh).
Do đó, tam giác AFE = tam giác DCE (theo trường hợp bằng nhau góc - cạnh - góc).
Suy ra EF = EC (hai cạnh tương ứng).
c) Chứng minh AD song song FC:

Cách 1: Sử dụng tính chất tam giác cân và góc đồng vị.

Vì BA = BD (giả thiết) nên tam giác ABD cân tại B.
Suy ra Góc BAD = Góc BDA.
Vì tam giác AFE = tam giác DCE (chứng minh ở câu b) nên AF = DC (hai cạnh tương ứng).
Ta có: BF = BA + AF và BC = BD + DC.
Mà BA = BD và AF = DC, suy ra BF = BC.
Do đó, tam giác BFC cân tại B.
Suy ra Góc BFC = Góc BCF.
Trong tam giác ABD cân tại B, Góc BDA = (180 độ - Góc ABC) / 2.
Trong tam giác BFC cân tại B, Góc BCF = (180 độ - Góc ABC) / 2.
Từ đó suy ra Góc BDA = Góc BCF.
Hai góc Góc BDA và Góc BCF đang ở vị trí đồng vị đối với hai đường thẳng AD và FC được cắt bởi đường thẳng BC.
Vậy AD song song với FC