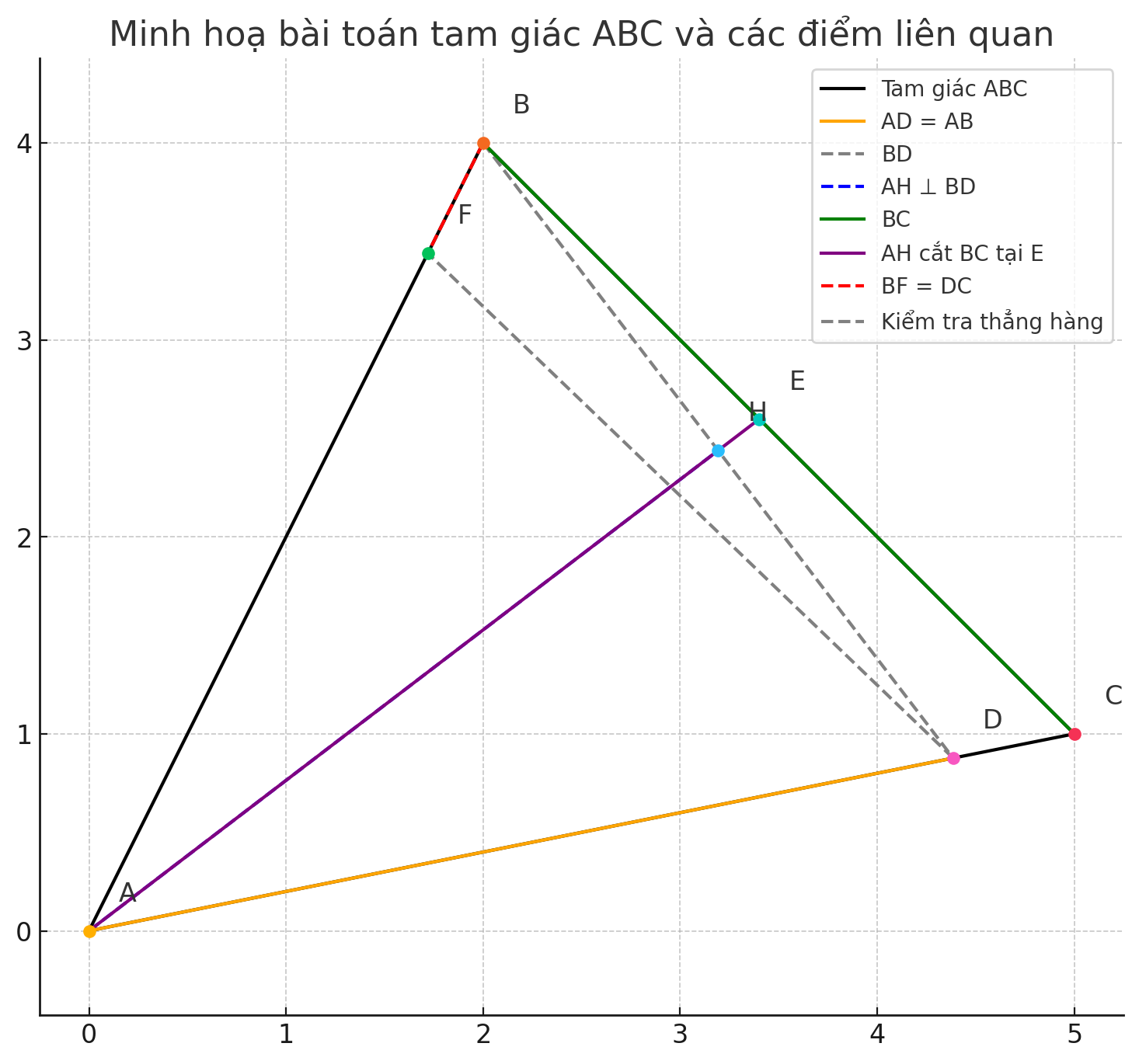
a) Chứng minh $\triangle AHB = \triangle AHD$

Xét hai tam giác $\triangle AHB$ và $\triangle AHD$:

- $AB = AD$ (giả thiết)
- $AH$ chung
- $\angle AHB = \angle AHD = 90^\circ$ (do $AH \perp BD$)

⇒ Hai tam giác vuông có:
- Cạnh huyền bằng nhau
- Cạnh góc vuông chung

$\Rightarrow \triangle AHB = \triangle AHD \quad (\text{c.g.c})$

b) Gọi E là giao điểm của $AH$ và $BC$. Chứng minh $EB = ED$, $AE$ là trung trực của $BD$

Từ a) có:
$\triangle AHB = \triangle AHD \Rightarrow HB = HD$

Mà $H$ nằm trên $BD$, nên $H$ là trung điểm của $BD$

$AH \perp BD$ và đi qua trung điểm $H$
⇒ $AH$ là đường trung trực của đoạn $BD$

⇒ Mọi điểm trên $AH$ cách đều $B$ và $D$

⇒ $E \in AH \Rightarrow EB = ED$, và $AE$ là đường trung trực của $BD$

c) Chứng minh $EC > EB$

Vì $E$ nằm trên $AH$, mà $AH$ cắt đoạn $BC$ tại $E$, nên:

- $E$ nằm giữa $B$ và $C$, gần $B$ hơn do $AB < AC$
- Mà $EB = ED$ và $D$ nằm trên $AC$, suy ra $EC = ED + DC > ED$

$\Rightarrow EC > EB$

d) Trên tia đối của $BA$ lấy điểm $F$ sao cho $BF = DC$. Chứng minh 3 điểm $D, E, F$ thẳng hàng

Ta xét hình học phản xạ:

- $AE$ là trung trực của $BD$
- $F$ được dựng đối xứng với $C$ qua $AE$, vì:
- $BF = DC$
- $AE \perp BD$, và chia đôi góc

Do đó:
- Tam giác $DCE$ phản xạ qua trục $AE$ → thành tam giác $EBF$

⇒ $D, E, F$ nằm trên cùng một đường thẳng

- a) $\triangle AHB = \triangle AHD$
- b) $EB = ED$, $AE$ là trung trực của $BD$
- c) $EC > EB$
- d) Ba điểm $D, E, F$ thẳng hàng

a) Chứng minh: △AHB = △AHD

Xét △AHB và △AHD có:

∠AHB = ∠AHD = 90° (vì AH ⊥ BD)
Cạnh AH là cạnh chung
AB = AD (giả thiết)
Suy ra △AHB = △AHD (theo trường hợp cạnh huyền - cạnh góc vuông).

b) Chứng minh: EB = ED và AE là đường trung trực của đoạn BD

Chứng minh EB = ED:

Vì △AHB = △AHD (chứng minh ở câu a), ta có:HB = HD (hai cạnh tương ứng)
∠BAH = ∠DAH (hai góc tương ứng)
Xét △EHB và △EHD có:HB = HD (chứng minh trên)
∠EHB = ∠EHD = 90° (vì AH ⊥ BD, E thuộc AH)
Cạnh EH là cạnh chung
Suy ra △EHB = △EHD (theo trường hợp cạnh - góc - cạnh).
Do đó, EB = ED (hai cạnh tương ứng).
Chứng minh AE là đường trung trực của đoạn BD:

Ta có HB = HD (chứng minh trên), nên H là trung điểm của BD.
Ta có AH ⊥ BD tại H, mà E nằm trên tia AH, nên AE ⊥ BD.
Vì AE vuông góc với BD tại trung điểm H của BD, nên AE là đường trung trực của đoạn thẳng BD.
Cách khác chứng minh AE là trung trực:

Ta có AB = AD (giả thiết). Nên điểm A cách đều hai đầu mút B và D.
Ta có EB = ED (chứng minh trên). Nên điểm E cách đều hai đầu mút B và D.
Tập hợp các điểm cách đều hai đầu mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
Vậy đường thẳng đi qua A và E chính là đường trung trực của đoạn thẳng BD.

c) Chứng minh: EC > EB

Trong △ABC, vì AB < AC (giả thiết), nên góc đối diện với cạnh AB nhỏ hơn góc đối diện với cạnh AC: ∠ACB < ∠ABC hay ∠C < ∠ABC.
Xét △ABE và △ADE có:AB = AD (giả thiết)
∠BAE = ∠DAE (vì ∠BAH = ∠DAH chứng minh ở câu b)
AE là cạnh chung
Suy ra △ABE = △ADE (cạnh - góc - cạnh).
Do đó, ∠ABE = ∠ADE (hai góc tương ứng).
Ta cần chứng minh EC > EB. Mà EB = ED (chứng minh ở câu b), vậy ta cần chứng minh EC > ED.
Xét △EDC. Để chứng minh EC > ED, ta cần chứng minh góc đối diện với EC lớn hơn góc đối diện với ED. Tức là ta cần chứng minh ∠EDC > ∠ECD (hay ∠EDC > ∠C).
Vì D nằm giữa A và C nên A, D, C thẳng hàng. Do đó, ∠ADE và ∠EDC là hai góc kề bù: ∠ADE + ∠EDC = 180°.
Suy ra ∠EDC = 180° - ∠ADE.
Mà ∠ADE = ∠ABE = ∠ABD (vì E nằm trên BC nên ∠ABE = ∠ABC không đúng, phải là ∠ABE = ∠ABD).
Vậy ∠EDC = 180° - ∠ABD.
Ta cần chứng minh 180° - ∠ABD > ∠C.
Điều này tương đương với 180° > ∠ABD + ∠C.
Xét △ABC có: ∠BAC + ∠ABC + ∠C = 180°. ∠BAC + (∠ABD + ∠EBC) + ∠C = 180°.
Do đó, 180° - (∠ABD + ∠C) = ∠BAC + ∠EBC.
Vậy, bất đẳng thức 180° > ∠ABD + ∠C tương đương với ∠BAC + ∠EBC > 0.
Vì △ABC là tam giác nhọn nên ∠BAC > 0.
Vì E là giao điểm của AH và BC, và H nằm giữa B và D, tia AH cắt BC tại E thì E nằm giữa B và C. Do đó ∠EBC > 0.
Vậy ∠BAC + ∠EBC > 0 là đúng.
Do đó, ∠EDC > ∠C là đúng.
Trong △EDC, vì ∠EDC > ∠C nên cạnh đối diện với ∠EDC lớn hơn cạnh đối diện với ∠C. Tức là EC > ED.
Mà ED = EB (chứng minh ở câu b).
Vậy EC > EB.

d) Chứng minh: Ba điểm D, E, F thẳng hàng

Xét △EBF và △EDC có:EB = ED (chứng minh ở câu b)
BF = DC (giả thiết)
Góc xen giữa:∠EBF: Vì F nằm trên tia đối của tia BA nên F, B, A thẳng hàng. Do đó ∠EBF và ∠EBA là hai góc kề bù. ∠EBF = 180° - ∠EBA. Mà E nằm trên BC, nên ∠EBA = ∠ABC? Không đúng. ∠EBA = ∠ABD. Vậy ∠EBF = 180° - ∠ABD.
∠EDC: Như đã chứng minh ở câu c, ∠EDC = 180° - ∠ADE. Mà ∠ADE = ∠ABE = ∠ABD (từ △ABE = △ADE). Vậy ∠EDC = 180° - ∠ABD.
Do đó, ∠EBF = ∠EDC.
Vậy △EBF = △EDC (theo trường hợp cạnh - góc - cạnh).
Suy ra ∠BEF = ∠DEC (hai góc tương ứng).
Ta có E là giao điểm của AH và BC, nên B, E, C thẳng hàng.
Do đó, ∠DEB + ∠DEC = 180° (hai góc kề bù).
Mà ∠DEC = ∠BEF (chứng minh trên).
Thay vào ta được: ∠DEB + ∠BEF = 180°.
Hai góc ∠DEB và ∠BEF là hai góc kề nhau có tổng bằng 180°, và có chung cạnh EB. Suy ra hai tia ED và EF là hai tia đối nhau.
Vậy ba điểm D, E, F thẳng hàng.
Kết luận: a) △AHB = △AHD (cạnh huyền - cạnh góc vuông) b) EB = ED và AE là đường trung trực của đoạn BD. c) EC > EB. d) Ba điểm D, E, F thẳng hàng.