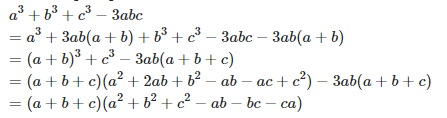Quảng cáo
3 câu trả lời 4099
\[\begin{array}{l}
\left( {a + b + c} \right).{\rm{ }}\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) = {a^3} + {b^3} + {c^3} - 3abc\\
xet:\\
VT = \left( {a + b + c} \right).{\rm{ }}\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right)\\
= {a^3} + a{b^2} + a{c^2} - {a^2}b - abc - {a^2}c + {a^2}b + {b^3} + b{c^2} - a{b^2} - {b^2}c - abc + {a^2}c + {b^2}c + {c^3} - abc - b{c^2} - a{c^2}\\
= {a^3} + {b^3} + {c^3} - 3abc = VP\\
vay:\left( {a + b + c} \right).{\rm{ }}\left( {{a^2} + {b^2} + {c^2} - ab - bc - ca} \right) = {a^3} + {b^3} + {c^3} - 3abc
\end{array}\]
(a+b+c).(a2+b2+c2−ab−bc−ca)=a3+b3+c3−3abcxet:VT=(a+b+c).(a2+b2+c2−ab−bc−ca)=a3+ab2+ac2−a2b−abc−a2c+a2b+b3+bc2−ab2−b2c−abc+a2c+b2c+c3−abc−bc2−ac2=a3+b3+c3−3abc=VPvay:(a+b+c).(a2+b2+c2−ab−bc−ca)=a3+b3+c3−3abc
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171
-
돈이없다 💸😭
435 điểm
-
반짝이는 달 420 điểm
-
야연 ✨
400 điểm
-
보고 싶어요
385 điểm
-
jet jet #
345 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
305 điểm
-
`d.`
285 điểm
-
Kiều Anh 170 điểm
-
Phát: ''đạp = niềm tin hả?''; t : ''🤫🧏''
135 điểm
-
`color{blue}text{이 글을 읽는 사람은 바보다.`베트남이 챔피언입니다.
105 điểm
-
Hung Hungdoan 100 điểm
-
baolam<3
70 điểm
-
Paris.khong.co.em...
70 điểm
-
Judy Hopps
60 điểm
Rút gọn
Bài viết mới nhất Lớp 8
-
3 năm trước8220
-
3 năm trước7732
-
3 năm trước6571
-
3 năm trước6459
-
3 năm trước6291
