Quảng cáo
2 câu trả lời 7198
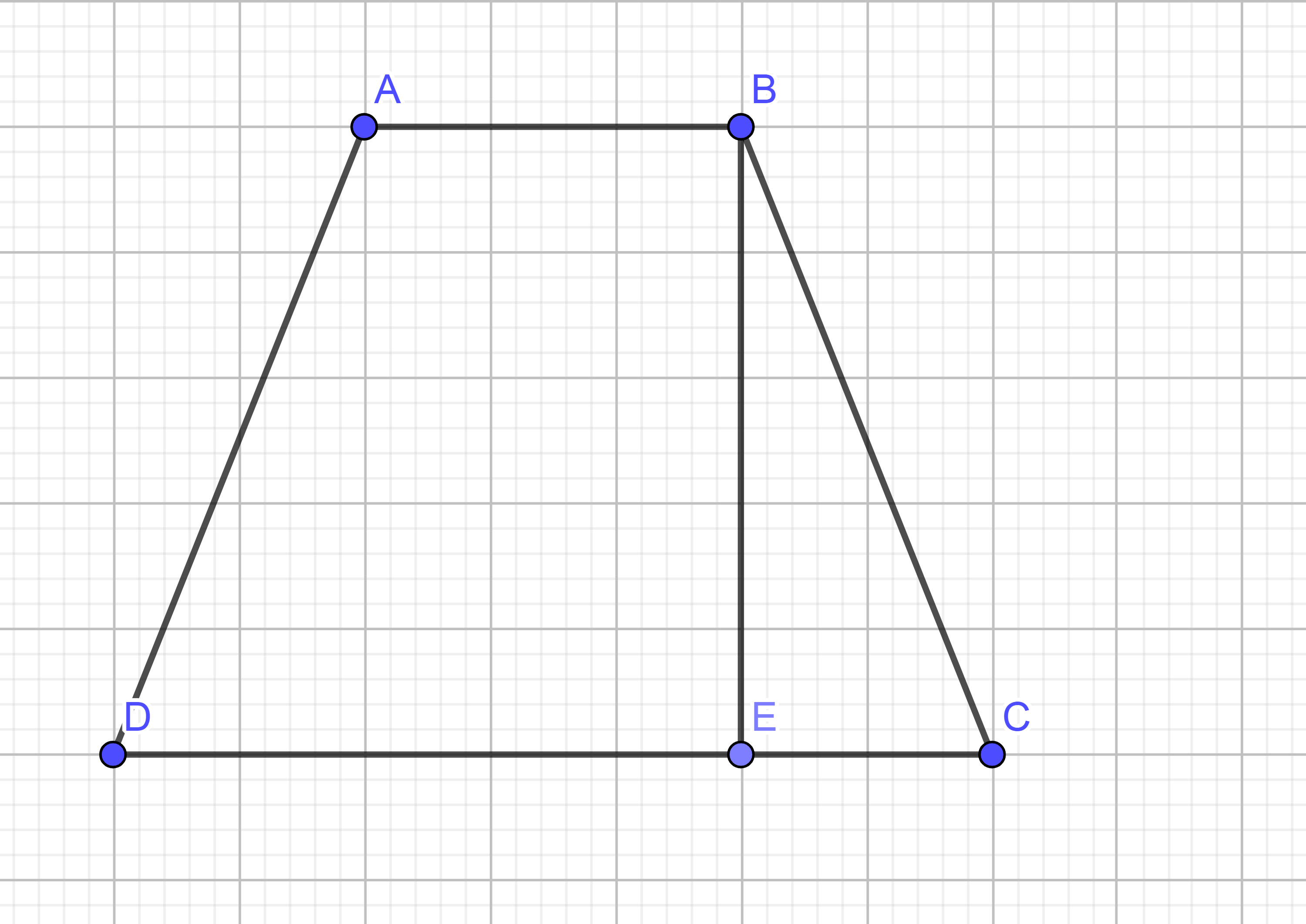
Kẻ BE vuông góc với CD
=>BE là chiều cao của hình thang
Ta có tứ giác ABCD là hình thang cân
=> EC=(CD-AB)/2=(24-10)/2=7(cm)
Xét tam giác vuông BEC
ÁP dụng Pytago ta có:
\(\begin{array}{l}
B{C^2} = B{E^2} + E{C^2}\\
= > BE = \sqrt {B{C^2} - E{C^2}} = \sqrt {{{25}^2} - {7^2}} = 24(cm)
\end{array}\)
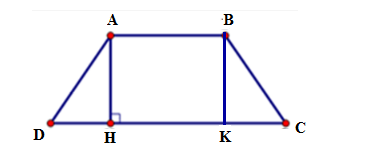
Từ A kẻ AH vuông góc với CD cắt CD tại H
Từ B kẻ BK vuông góc với CD cắt CD tại K
Ta có AB//CD
Mà H, K ∈ CD
Suy ra: AB//HK
Tứ giác ABKH có AB//HK
Suy ra: ABKH là hình thang
Ta có: AH ⊥ CD
BK ⊥CD
Suy ra AH//BK
Hình thang ABKH có 2 cạnh bên AH//BK
=> AH=BK, AB=HK=10cm
Do ABCD là hình thang cân nên 2 cạnh bên AD=BC=25cm.
Xét 2 tam giác vuông AHD và BKC có:
AH=BK (cmt)
AD=BC (gt)
⇒ΔAHD=ΔBKC(ch−cgv)
⇒DH=CK⇒DH=CK (2 cạnh tương ứng)
Ta có: DH+HK+CK=DC
=> DH+10+CK=24
=>DH+CK=24-10
=>DH+CK=14cm
=> DH=CK=14:2
=>DH=CK=7 (cm)
Áp dụng định lý Py-ta-go vào ΔAHDΔAHD ta có:
AD^2=AH^2+DH^2
⇒AH^2=25^2−7^2
⇒AH^2=625−49
⇒AH^2=576
⇒AH=24⇒AH=24cm
Vậy độ dài đường cao của hình thang cân ABCD là 24cm
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171
-
우옌🖤 해영 ✨
1810 điểm
-
Sori
1745 điểm
-
사랑해요😘
1190 điểm
-
Dương Nguyễn
1140 điểm
-
`color{blue}text{HuyTùng☢`
925 điểm
-
그림 그리기를 좋아하지만, 직업이 허락하지 않아요😞
875 điểm
-
하루토 [팜 안 둥]
850 điểm
-
돈이없다 💸😭
845 điểm
-
`d.`
805 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
785 điểm
-
🌷김은✨
630 điểm
-
Bích Hồng 625 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
585 điểm
-
jamJames 🥵👍
555 điểm
-
''e thik biker hơn a''
480 điểm
Rút gọn
Bài viết mới nhất Lớp 8
-
3 năm trước8220
-
3 năm trước7732
-
3 năm trước6571
-
3 năm trước6459
-
3 năm trước6291
