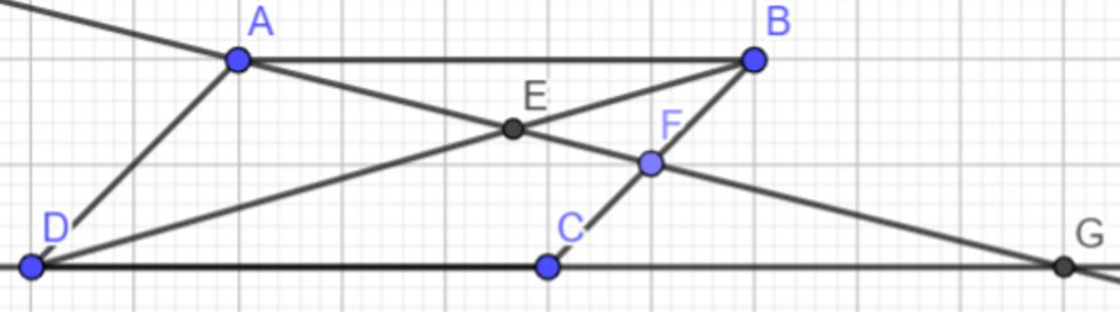
Cho hình bình hành ABCD. Trên cạnh BC lấy điểm F. Tia AF cắt BD và DC lần lượt tại B và G. Chứng minh:
a, Tam giác BEF đồng dạng với tam giác DEA, Tam giác DGE đồng dạng với tam giác BAE.
b,
c, BF.DG không đổi khi F thay đổi trên BC.
Quảng cáo
2 câu trả lời 29256
a) Xét $\Delta BEF$ và $\Delta DEA$
Có: $\widehat{E_{1}}=\widehat{E_{3}} (gt)$
$\widehat{ADE}=\widehat{FBE} (gt)$
$=>\Delta BEF $~$\Delta DEA (g-g)$
Xét $\Delta DGE $và $\Delta BAE$
Có: $\widehat{E_{2}}=\widehat{E_{4}} (gt)$
$\widehat{ABE}=\widehat{GDE} (gt)$
=> $\Delta DGE$~ $\Delta BAE (g-g)$
b)$ \Delta BEF$~$\Delta DEA$
$=>\frac{BE}{DE}=\frac{EF}{EA} (1)$
$\Delta BAE$~ $\Delta DGE$
$=>\frac{BE}{DE}=\frac{AE}{GE} (2)$
Từ (1) và (2)$=> \frac{AE}{GE}=\frac{EF}{EA}$
$=> AE^{2}=EF.EG$
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191