Cho tam giác ABC (AB < AC), có ba góc nhọn nội tiếp trong đường tròn tâm O, bán kính R. Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC.
1. Chứng minh rằng AEHF và AEDB là các tứ giác nội tiếp đường tròn.
2. Vẽ đường kính AK của đường tròn (O). Chứng minh tam giác ABD và tam giác AKC đồng dạng với nhau. Suy ra AB.AC = 2R.AD
3. Chứng minh rằng OC vuông góc với DE.
Quảng cáo
1 câu trả lời 11360
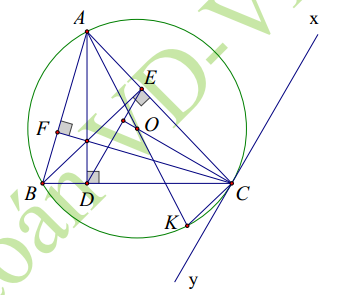
1. Ta có: và
Do đó: . Mà đây là hai góc đối nhau
tứ giác AEHF nội tiếp đường tròn
Ta lại có:
E và D cùng nhìn cạnh AB dưới một góc vuông.
Vậy tứ giác AEDB nội tiếp được.
2. Ta có: (góc nội tiếp chắn nửa đường tròn)
Hai tam giác vuông ADB và ACK có:
(góc nội tiếp cùng chắn cung AC)
Suy ra
0
3. Vẽ tiếp tuyến xy tại C của (O)
Ta có: 1
Mặt khác, AEDB nội tiếp
2 mà 3 nên 4
Từ (1) và (2) ta có: 5
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490


