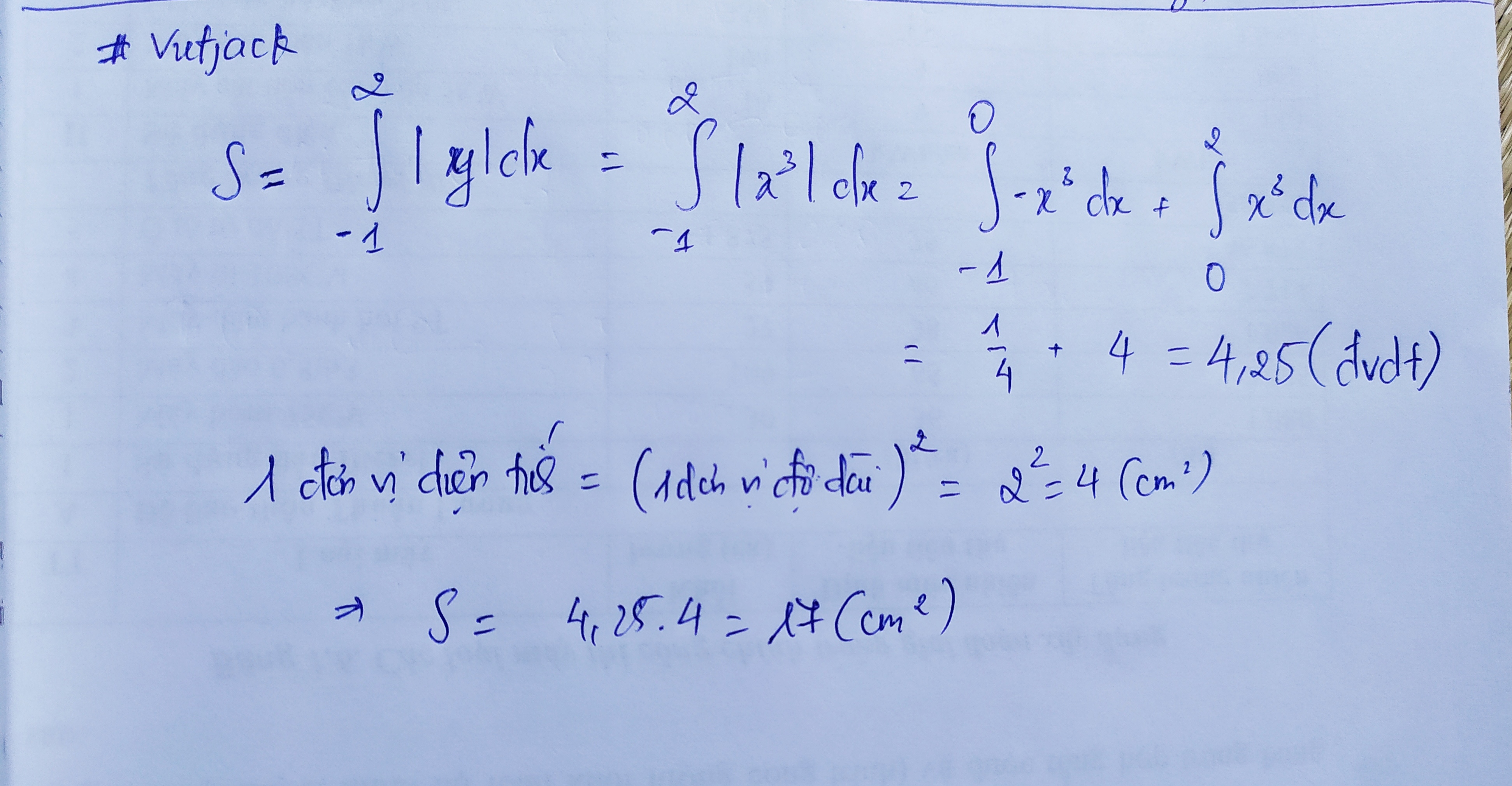Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x^3,trục hoành và hai đường thẳng x=-1,x=2 biết rằng mỗi đơn vị độ dài trên các trục tọa độ là 2cm
Quảng cáo
7 câu trả lời 4301
Để giải bài toán này, ta giả sử:
- Tổng số tiền trong hóa đơn là \( S \).
- Mỗi người sẽ phải trả số tiền là \( \frac{S}{8} \).
- Do Tuấn quên tiền, nên 7 người còn lại sẽ phải trả \( \frac{S}{7} \).
Theo đề bài, mỗi bạn trong 7 người còn lại phải trả thêm 25.000 đồng so với số tiền mỗi người phải trả nếu có Tuấn. Do đó, ta có được phương trình sau:
\[
\frac{S}{7} = \frac{S}{8} + 25000
\]
Giải phương trình này:
1. Nhân cả hai bên với 56 (bội số chung nhỏ nhất của 7 và 8) để loại bỏ mẫu:
\[
56 \cdot \frac{S}{7} = 56 \cdot \frac{S}{8} + 56 \cdot 25000
\]
2. Rút gọn:
\[
8S = 7S + 1400000
\]
3. Trừ \( 7S \) từ cả hai bên:
\[
S = 1400000
\]
Vậy tổng hóa đơn của bữa ăn trị giá là **1.400.000 đồng**.
`S = \int_{-1}^2 |x^3| dx`
Vì $x^3 < 0$ khi $x < 0$ và $x^3 \ge 0$ khi $x \ge 0$, chia tích phân thành hai phần:
`S = \int_{-1}^0 -x^3 dx + \int_0^2 x^3 dx`
`S = \left[-\frac{x^4}{4}\right]_{-1}^0 + \left[\frac{x^4}{4}\right]_0^2`
`S = \left(0 - \left(-\frac{(-1)^4}{4}\right)\right) + \left(\frac{2^4}{4} - 0\right)`
`S = \frac{1}{4} + \frac{16}{4}`
`S = \frac{17}{4}`
`S' = \frac{17}{4} \times (2 \text{ cm})^2 = \frac{17}{4} \times 4 \text{ cm}^2 = 17 \text{ cm}^2`
Vậy ....
\[A = \int_{-1}^{2} y \, dx = \int_{-1}^{2} x^3 \, dx\]
\[A = \left[ \frac{x^4}{4} \right]_{-1}^{2} = \frac{2^4}{4} - \frac{(-1)^4}{4} = \frac{16}{4} - \frac{1}{4} = 4 - \frac{1}{4} = \frac{16 - 1}{4} = \frac{15}{4}\]
\[A_{cm^2} = A \times (2 \, cm)^2 = \frac{15}{4} \times 4 = 15 \, cm^2\]
Để trả lời các câu hỏi về đồ thị trong không gian và đặc biệt là liên quan đến các tia trên mặt phẳng tọa độ, chúng ta có thể hình dung và vẽ một hình ảnh đơn giản.
### Hình vẽ:
1. Vẽ trục tọa độ (trục x và trục y).
2. Đánh dấu điểm O (góc tọa độ gốc) tại tọa độ (0, 0).
3. Trên tia Ox, đánh dấu điểm A tại tọa độ (2, 0).
4. Trên tia Oy, đánh dấu điểm B tại tọa độ (0, 5).
```
B(0, 5)
|
|
|
O(0,0)-------------A(2,0)
|
|
```
### a. Trên hình vẽ có mấy tia? Đó là những tia nào?
- **Có 5 tia** trên hình vẽ:
1. Tia OA (từ điểm O đến A)
2. Tia OB (từ điểm O đến B)
3. Tia Ox (từ O qua A, kéo dài về phía bên phải)
4. Tia Oy (từ O qua B, kéo dài lên trên)
5. Tia AB (từ A đến B, không kéo dài, chỉ là đoạn thẳng)
### b. Tia Ax và By có đối nhau không? Vì sao?
- **Không, tia Ax và By không đối nhau.**
- Tia Ax là tia kéo dài từ A theo hướng trục x (hướng bên phải).
- Tia By là tia kéo dài từ B theo hướng trục y (hướng lên trên).
- Hai tia này không đi qua nhau và không nằm trên cùng một đường thẳng, do đó chúng không đối nhau.
### c. Tính độ dài đoạn thẳng AB (vẽ cả hình)
- Để tính độ dài đoạn thẳng AB, chúng ta có thể sử dụng định lý Pythagore trong tam giác vuông OAB.
1. **Độ dài OA = 2 cm** (trên trục x).
2. **Độ dài OB = 5 cm** (trên trục y).
Đoạn thẳng AB có thể tính bằng công thức:
\[
AB = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}
\]
Thay tọa độ của A và B:
- Tọa độ A (2, 0)
- Tọa độ B (0, 5)
\[
AB = \sqrt{(0 - 2)^2 + (5 - 0)^2} = \sqrt{(-2)^2 + (5)^2} = \sqrt{4 + 25} = \sqrt{29}
\]
- Do đó, độ dài đoạn thẳng AB là:
\[
AB \approx 5.385 \text{ cm}
\]
**Hình vẽ hoàn chỉnh** sẽ mô tả các điểm và độ dài của đoạn thẳng AB.
Hy vọng những thông tin này sẽ giúp ích cho bạn trong việc hiểu bài toán và làm việc với đồ thị! Nếu bạn cần thêm hỗ trợ, hãy cho tôi biết nhé.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129857
Đã trả lời bởi chuyên gia
129857 -
 Đã trả lời bởi chuyên gia
104336
Đã trả lời bởi chuyên gia
104336 -
 Đã trả lời bởi chuyên gia
94255
Đã trả lời bởi chuyên gia
94255 -
 Đã trả lời bởi chuyên gia
70288
Đã trả lời bởi chuyên gia
70288