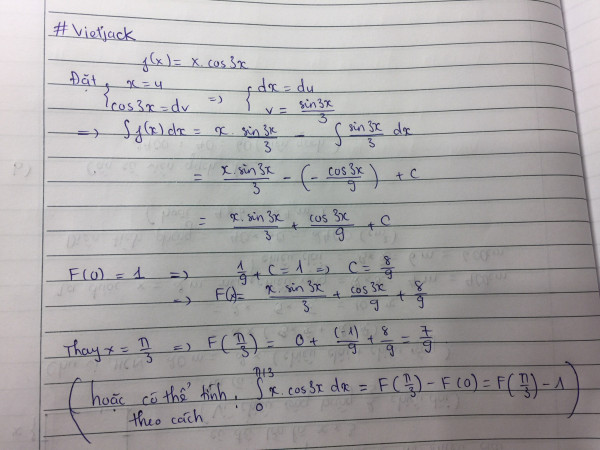Để tìm giá trị của \(F\left(\frac{\pi}{3}\right)\), ta cần tính nguyên hàm của hàm số \(f(x) = x \cos(3x)\).

Đầu tiên, sử dụng phương pháp tích phân từng phần:

Cho \(u = x\) và \(dv = \cos(3x)dx\),
- Khi đó, \(du = dx\) và \(v = \frac{\sin(3x)}{3}\).

Áp dụng công thức tích phân từng phần:
\[ \int u \, dv = uv - \int v \, du \]

Ta có:
\[ \int x \cos(3x) \, dx = x \cdot \frac{\sin(3x)}{3} - \int \frac{\sin(3x)}{3} \, dx \]
\[ = \frac{x \sin(3x)}{3} - \frac{1}{3} \int \sin(3x) \, dx \]

Tính tiếp \( \int \sin(3x) \, dx \):
\[ \int \sin(3x) \, dx = -\frac{\cos(3x)}{3} \]

Do đó:
\[ \int x \cos(3x) \, dx = \frac{x \sin(3x)}{3} + \frac{\cos(3x)}{9} + C \]

Gọi \(F(x)\) là nguyên hàm của \(f(x)\):
\[ F(x) = \frac{x \sin(3x)}{3} + \frac{\cos(3x)}{9} + C \]

Sử dụng điều kiện \(F(0) = 1\):
\[ F(0) = \frac{0 \cdot \sin(0)}{3} + \frac{\cos(0)}{9} + C = 1 \]
\[ \frac{1}{9} + C = 1 \]
\[ C = 1 - \frac{1}{9} \]
\[ C = \frac{8}{9} \]

Vậy:
\[ F(x) = \frac{x \sin(3x)}{3} + \frac{\cos(3x)}{9} + \frac{8}{9} \]

Cuối cùng, tính \(F\left(\frac{\pi}{3}\right)\):
\[ F\left(\frac{\pi}{3}\right) = \frac{\frac{\pi}{3} \sin\left(3 \cdot \frac{\pi}{3}\right)}{3} + \frac{\cos\left(3 \cdot \frac{\pi}{3}\right)}{9} + \frac{8}{9} \]
\[ = \frac{\frac{\pi}{3} \sin(\pi)}{3} + \frac{\cos(\pi)}{9} + \frac{8}{9} \]
\[ = \frac{\frac{\pi}{3} \cdot 0}{3} + \frac{-1}{9} + \frac{8}{9} \]
\[ = 0 - \frac{1}{9} + \frac{8}{9} \]
\[ = \frac{7}{9} \]

Do đó, giá trị của \(F\left(\frac{\pi}{3}\right)\) là \(\frac{7}{9}\).