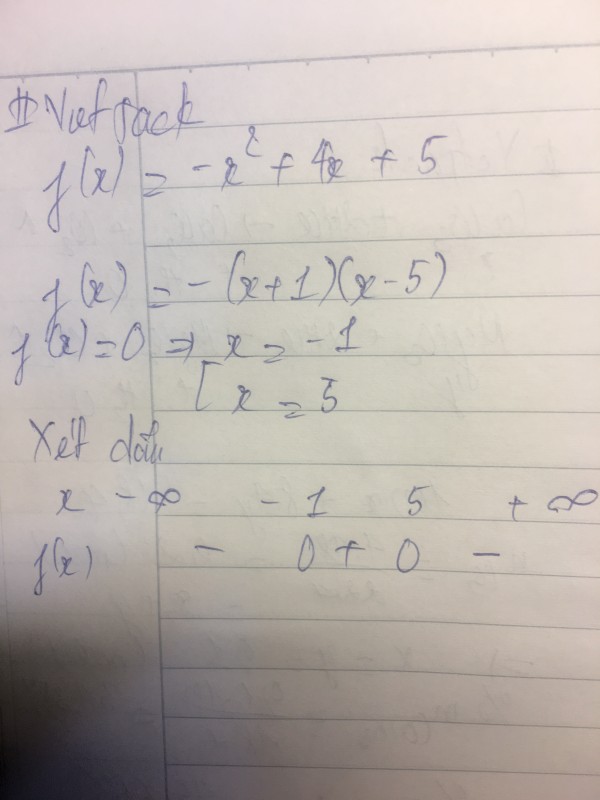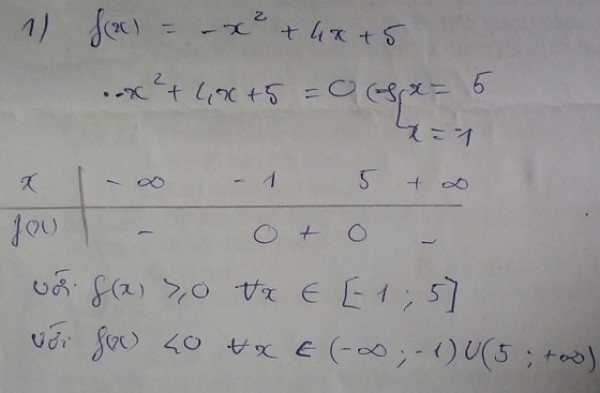Quảng cáo
6 câu trả lời 3658
`-x² + 4x + 5 = 0`
Tính $\Delta'$ (delta phẩy):
$\Delta'$ = $b'^2$ - ac = $2^2$ - (-1) * 5 = 9 > 0
Vì $\Delta'$ > 0, phương trình có 2 nghiệm phân biệt:
$x_1$ = $\frac{-b' + \sqrt{\Delta'}}{a}$ = $\frac{-2 + 3}{-1}$ = -1
$x_2$ = $\frac{-b' - \sqrt{\Delta'}}{a}$ = $\frac{-2 - 3}{-1}$ = 5
Dựa vào bảng xét dấu, ta có:
`f(x) < 0` khi x $\in$ (-∞; -1) $\cup$ (5; +∞)
`f(x) > 0 `khi x $\in$ (-1; 5)
`f(x) = 0 `khi x = -1 hoặc x = 5
Vậy, dấu của biểu thức f(x) = -x² + 4x + 5 như sau:
Âm trên khoảng `(-∞; -1) `và` (5; +∞)`
Dương trên khoảng `(-1; 5)`
Bằng 0 tại x = -1 và x = 5.
Quê nhà trong gió chiều
Chiều buông sương mỏng lối quê xa,
Gió ru bờ bãi, nắng nhòa mái rạ.
Khói lam lặng lẽ vờn hiên nhà,
Mẹ ngồi chờ gió hong màu
(- 6 + x) - [17 - (3 - x) + 4]
= - 6 + x - (17 - 3 + x + 4)
= - 6 + x - 17 + 3 - x - 4
= (x - x) + (- 6 - 17 + 3 - 4)
= - 24
$f(x) = 0$ tại $x = -1$ và $x = 5$.
$f(x) > 0$ với mọi $x \in (-1; 5)$.
$f(x) < 0$ với mọi $x \in (-\infty; -1) \cup (5; +\infty)$.
Quảng cáo
Bạn hỏi - Chuyên gia trả lời
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Đã trả lời bởi chuyên gia
90843 -
Đã trả lời bởi chuyên gia
61357
-
Đã trả lời bởi chuyên gia
51612
-
Đã trả lời bởi chuyên gia
39445
-
MÈO RBX
620 điểm
-
Đang rặn.
510 điểm
-
vợ việt gu sì ki bi đi toi lét🥵
415 điểm
-
thanh y
375 điểm
-
Ctrl+C Ctrl+V
325 điểm
-
𝑲𝒊𝒕𝒕𝒚
295 điểm
-
Nói lắm thế
285 điểm
-
DẠI LÊ 235 điểm
-
NghGiang
230 điểm
-
Chán đời.
225 điểm
-
Duy Phạm 215 điểm
-
Tôi rất mê cờ vua 185 điểm
-
★꧁☁︎જ⁀➴✞༺S͜͡øN͜͡G͜͡ ༒︎ N͜͡G͜͡ư༻✞જ⁀➴☁︎꧂★
145 điểm
Rút gọn
