cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB=a ,AD=a căn 2,SA vuông góc với (ABCD) .gọi M là trung điểm của AD ,I là giao điểm của AC và BM.CMR: SAC vuông góc vói SMB
Quảng cáo
7 câu trả lời 41539
$AB=CD=a\\ AD=BC=a\sqrt{2}\\ AC=\sqrt{AB^2+BC^2}=a\sqrt{3}\\ AM=\dfrac{\sqrt{2}}{2}\\ BM=\sqrt{AB^2+AM^2}=a\dfrac{\sqrt{6}}{2}\\ \cos(\widehat{CAB})=\dfrac{CA^2+AB^2-BC^2}{2CA.AB}=\dfrac{\sqrt{3}}{3}\\ \cos(\widehat{ABM})=\dfrac{AB^2+BM^2-AM^2}{2AB.BM}=\dfrac{\sqrt{6}}{3}\\ \widehat{AIB}=180^o-\widehat{CAB}-\widehat{ABM}\\ =180^o-\arccos\left(\dfrac{\sqrt{3}}{3}\right)-\arccos\left(\dfrac{\sqrt{6}}{3}\right)\\ =90^o\\ \Rightarrow MB \perp AC\\ \text{Mà} \,\,MB \perp SA(SA \perp (ABCD))\\ \Rightarrow MB \perp (SAC)\\ \Rightarrow (SMB) \perp (SAC)$
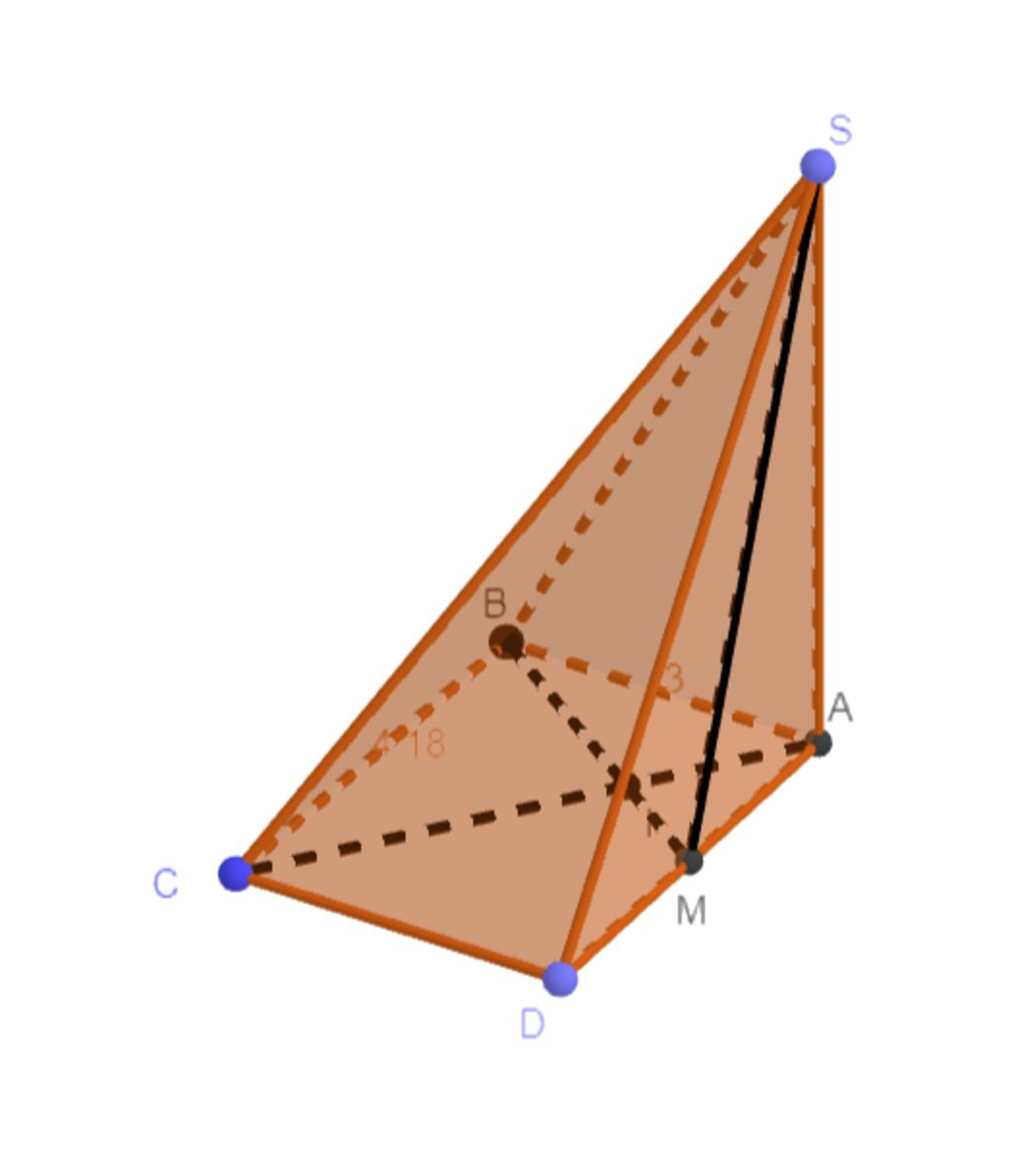

Áp dụng Pytago ta có:
$AC=\sqrt{AB^2+BC^2}=a\sqrt 3$
$BM=\sqrt{AB^2+AM^2}=\dfrac{a\sqrt 6}{2}$
Gọi $AC \cap BD = \{O\}$ vì $I$ là giao điểm của hai đường trung tuyến $AO$ và $BM$
$\rightarrow O$ là trong tâm của $\Delta ABD$
$AI=\dfrac23AO=\dfrac{a\sqrt 3}{3}$
$BI=\dfrac23BM=\dfrac{a\sqrt 6}{3}$
Ta có: $AB^2=AI^2+BI^2$
$\rightarrow \Delta ABI ⊥ I$
$\rightarrow \begin{cases}BM ⊥ AI\\SA⊥BM \end{cases}\to BM ⊥ (SAC) \to (SBM)⊥(SAC)$
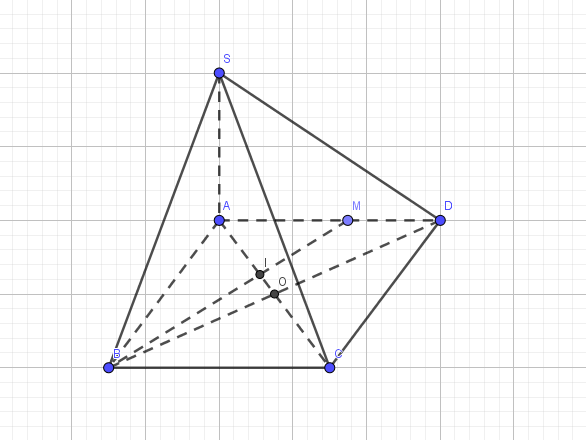
Áp dụng Pytago ta có:
AC=√AB2+BC2=a√3AC=AB2+BC2=a3
BM=√AB2+AM2=a√62BM=AB2+AM2=a62
Gọi AC∩BD={O}AC∩BD={O} vì II là giao điểm của hai đường trung tuyến AOAO và BMBM
→O→O là trong tâm của ΔABDΔABD
AI=23AO=a√33AI=23AO=a33
BI=23BM=a√63BI=23BM=a63
Ta có: AB2=AI2+BI2AB2=AI2+BI2
→ΔABI⊥I→ΔABI⊥I
→{BM⊥AISA⊥BM→BM⊥(SAC)→(SBM)⊥(SAC)
Áp dụng Pytago ta có:
AC=√AB2+BC2=a√3AC=AB2+BC2=a3
BM=√AB2+AM2=a√62BM=AB2+AM2=a62
Gọi AC∩BD={O}AC∩BD={O} vì II là giao điểm của hai đường trung tuyến AOAO và BMBM
→O→O là trong tâm của ΔABDΔABD
AI=23AO=a√33AI=23AO=a33
BI=23BM=a√63BI=23BM=a63
Ta có: AB2=AI2+BI2AB2=AI2+BI2
→ΔABI⊥I→ΔABI⊥I
→{BM⊥AISA⊥BM→BM⊥(SAC)→(SBM)⊥(SAC)
Áp dụng Pytago ta có:
AC=√AB2+BC2=a√3AC=AB2+BC2=a3
BM=√AB2+AM2=a√62BM=AB2+AM2=a62
Gọi AC∩BD={O}AC∩BD={O} vì II là giao điểm của hai đường trung tuyến AOAO và BMBM
→O→O là trong tâm của ΔABDΔABD
AI=23AO=a√33AI=23AO=a33
BI=23BM=a√63BI=23BM=a63
Ta có: AB2=AI2+BI2AB2=AI2+BI2
→ΔABI⊥I→ΔABI⊥I
→{BM⊥AISA⊥BM→BM⊥(SAC)→(SBM)⊥(SAC)
Áp dụng Pytago ta có:
AC=√AB2+BC2=a√3AC=AB2+BC2=a3
BM=√AB2+AM2=a√62BM=AB2+AM2=a62
Gọi AC∩BD={O}AC∩BD={O} vì II là giao điểm của hai đường trung tuyến AOAO và BMBM
→O→O là trong tâm của ΔABDΔABD
AI=23AO=a√33AI=23AO=a33
BI=23BM=a√63BI=23BM=a63
Ta có: AB2=AI2+BI2AB2=AI2+BI2
→ΔABI⊥I→ΔABI⊥I
→{BM⊥AISA⊥BM→BM⊥(SAC)→(SBM)⊥(SAC
Quảng cáo
Bạn muốn hỏi bài tập?


