Quảng cáo
4 câu trả lời 1449
Ta có:
$alog_2 5 = 4 \Rightarrow a = \frac{4}{\log_2 5} = \frac{4}{\frac{\log 5}{\log 2}} = \frac{4 \log 2}{\log 5}$
$blog_4 6 = 16 \Rightarrow b = \frac{16}{\log_4 6} = \frac{16}{\frac{\log 6}{\log 4}} = \frac{16 \log 4}{\log 6} = \frac{16 \cdot 2 \log 2}{\log 6} = \frac{32 \log 2}{\log 6}$
$clog_7 3 = 49 \Rightarrow c = \frac{49}{\log_7 3} = \frac{49}{\frac{\log 3}{\log 7}} = \frac{49 \log 7}{\log 3}$
Thay vào biểu thức T, ta được:
$T = a^[(log2 5)^2] + b^[(log4 6)^2)] +3c^[(log7 3)^2)] $
$ = (\frac{4 \log 2}{\log 5})^[(log2 5)^2] + (\frac{32 \log 2}{\log 6})^[(log4 6)^2)] + 3 (\frac{49 \log 7}{\log 3})^[(log7 3)^2)]$
$= 4^{[(log2 5)^2]} + 32^{[(log4 6)^2)]} + 3 \cdot 49^{[(log7 3)^2)]} $
$ = 2^{2[(log2 5)^2]} + 2^{5[(log4 6)^2)]} + 3 \cdot 7^{2[(log7 3)^2)]}$
$\log_a b = \frac{\log b}{\log a}$
$\log_a a = 1$
Ta có:
$(\log_2 5)^2 = (\frac{\log 5}{\log 2})^2 = \frac{(\log 5)^2}{(\log 2)^2}$
$(\log_4 6)^2 = (\frac{\log 6}{\log 4})^2 = (\frac{\log 6}{2 \log 2})^2 = \frac{(\log 6)^2}{4 (\log 2)^2}$
$(\log_7 3)^2 = (\frac{\log 3}{\log 7})^2 = \frac{(\log 3)^2}{(\log 7)^2}$
Thay vào biểu thức T,
$T = 2^{2 \cdot \frac{(\log 5)^2}{(\log 2)^2}} + 2^{5 \cdot \frac{(\log 6)^2}{4 (\log 2)^2}} + 3 \cdot 7^{2 \cdot \frac{(\log 3)^2}{(\log 7)^2}}$
$= 2^{\frac{2 (\log 5)^2}{(\log 2)^2}} + 2^{\frac{5 (\log 6)^2}{4 (\log 2)^2}} + 3 \cdot 7^{\frac{2 (\log 3)^2}{(\log 7)^2}}$
Kết quả cuối cùng là:
$T = 2^{\frac{2 (\log 5)^2}{(\log 2)^2}} + 2^{\frac{5 (\log 6)^2}{4 (\log 2)^2}} + 3 \cdot 7^{\frac{2 (\log 3)^2}{(\log 7)^2}}$
bấm máy tính
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129868
Đã trả lời bởi chuyên gia
129868 -
 Đã trả lời bởi chuyên gia
104349
Đã trả lời bởi chuyên gia
104349 -
 Đã trả lời bởi chuyên gia
94270
Đã trả lời bởi chuyên gia
94270 -
 Đã trả lời bởi chuyên gia
70373
Đã trả lời bởi chuyên gia
70373

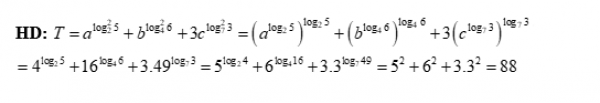
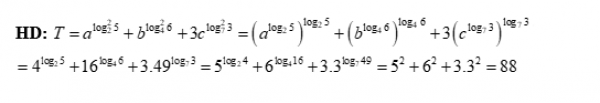 M
M

