Cho ba điểm A , B , C trên một đường thẳng theo thứ tự ấy và đường thẳng (d) vuông góc với AC tại A . Vẽ đường tròn đường kính BC và trên đó lấy điểm M bất kì . Tia CM cắt đường thẳng d tại D ; tia AM cắt đường tròn tại điểm thứ hai N ; tia DB cắt đườngCtròn tại điểm thứ hai P.
a) CMR tứ giác ABMD nội tiếp được
b) CMR : CM.CD không phụ thuộc vị trí của M
c) Tứ giác APND là hình gì ? Tại sao ?
d) Chứng minh trọng tâm G của tam giác MAC chạy trên một đường tròn cố định
Quảng cáo
1 câu trả lời 73
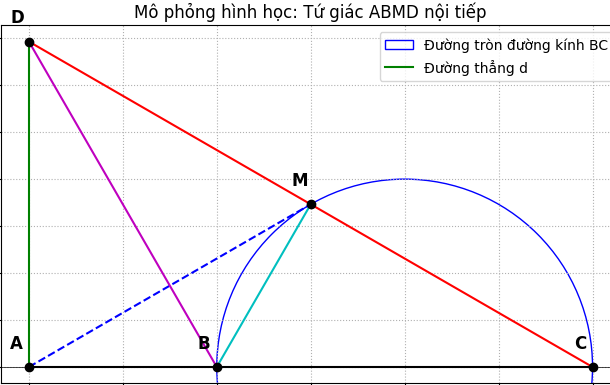
a) Chứng minh tứ giác ABMD nội tiếp
- Vì M nằm trên đường tròn đường kính BC nên góc (góc nội tiếp chắn nửa đường tròn).
=> (kề bù với ).
- Theo giả thiết, đường thẳng d AC tại A, nên .
- Xét tứ giác ABMD, ta có . Hai đỉnh A và M cùng nhìn đoạn BD dưới một góc vuông.
=> Tứ giác ABMD nội tiếp đường tròn đường kính BD.
b) Chứng minh CM CD không phụ thuộc vị trí của M
- Xét hai tam giác CMA và CAD, ta có:
Góc chung.
(như đã chứng minh ở câu a).
(do d AC).
Do đó, CMA CAD (g.g).
Lập tỉ số đồng dạng: .
=> CM.CD = CA2.
- Vì A và C cố định nên độ dài CA không đổi. Vậy CM.CD không đổi.
c) Tứ giác APND là hình gì?
- Tứ giác APND là hình thang cân.
- Ta có (góc nội tiếp chắn nửa đường tròn), nên CP DB. Trong tam giác BCD, CP và DA là hai đường cao cắt nhau tại M (vì DA BC và CP DB). Vậy M là trực tâm BCD => BM CD.
- Mà . Từ đó ta chứng minh được các cặp cạnh song song dựa trên góc nội tiếp (hoặc chứng minh APND nội tiếp và có hai cạnh đáy song song).
- Cụ thể: DN // AP vì cùng vuông góc với một phương nhất định hoặc dựa vào tính chất trực tâm.
d) Quỹ tích trọng tâm G của tam giác MAC
- Gọi I là trung điểm của AC. Vì A, C cố định nên I cố định.
- Theo tính chất trọng tâm: (hoặc hiểu theo độ dài đại số trên tia IM sao cho IG = ).
- Đây là phép vị tự tâm I tỉ số k = biến điểm M thành điểm G.
- Vì M chạy trên đường tròn đường kính BC (gọi tâm là O, bán kính R = BC/2), nên G sẽ chạy trên một đường tròn là ảnh của đường tròn (O) qua phép vị tự này.
Vậy: Trọng tâm G chạy trên một đường tròn cố định.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
104515
Đã trả lời bởi chuyên gia
104515 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
69452
Đã trả lời bởi chuyên gia
69452 -
 Đã trả lời bởi chuyên gia
57398
Đã trả lời bởi chuyên gia
57398 -
 Đã trả lời bởi chuyên gia
47987
Đã trả lời bởi chuyên gia
47987 -
 Đã trả lời bởi chuyên gia
46330
Đã trả lời bởi chuyên gia
46330 -
 Đã trả lời bởi chuyên gia
37376
Đã trả lời bởi chuyên gia
37376 -
 Đã trả lời bởi chuyên gia
36313
Đã trả lời bởi chuyên gia
36313


